AVL Tree

Angelia
2301854492
COMP6048 - CB01

Setelah mengikuti perkuliahan online melalui video conference, telah dibahas materi mengenai AVL Tree. Berikut ini pembahasan rangkuman mengenai materi AVL Tree.

Konsep dasarnya berawal dari kelemahan Binary Search Tree. Jika kita selalu menginsert data yang lebih besar, maka tree menjadi tidak seimbang karena anak cabang kanan akan lebih panjang daripada kiri. Hal ini akan membuat waktu pencarian data menjadi lebih lama. Untuk itu, dengan menggunakan AVL Tree sebagai salah satu solusi tree untuk mengatasi ketidakseimbangan anak cabang dapat teratasi sehingga waktu pencarian data akan lebih efisien.

   

                                      Hasil BST Tree                                     Hasil AVL Tree

AVL Tree merupakan self-balancing BST pertama yang ditemukan. Tree ini ditemukan oleh G.M. Adelson - Veleskii dan E.M. Landis.

Konsep AVL Tree
Cabang dinyatakan balance apabila jumlah anak kiri/kanan - jumlah anak kanan/kiri hasilnya tidak lebih dari 1. Jika perbedaan jumlah anak cabang kiri dan kanan lebih dari 1, maka tree dinyatakan tidak balance.

Kemudian, proses pengecekan tree balance adalah dengan mengecek dari urutan terbawah lalu naik ke atas. Jika ditemukan parent memiliki anak cabang yang tidak balance maka akan dilakukan rotation untuk mengubah tree agar menjadi balance.

Penerapan AVL Tree

• Insertion

Berikut ini langkah melakukan insertion pada AVL Tree:

1. Melakukan insert dengan konsep seperti BST.

2. Dilakukan pengecekan terhadap jalur dari penginputan node hingga ke root, apakah ada parent tree yang memiliki jumlah anak cabang yang tidak seimbang, maka tree akan dibuat balance dengan melakukan rotation.

• Deletion

Berikut ini langkah melakukan deletion pada AVL Tree:

1. Dilakukan prosedur delete node sesuai konsep BST.

2. Dilakukan pengecekan balance tree pada parent dari node yang di delete hingga ke root. Jika tidak seimbang, maka dilakukan rotation.

Penerapan Rebalance AVL Tree

• Single Rotation

Dilakukan jika anak cabang dari node yang dimasukkan yang tidak balance sejalur dengan root (left-left atau right-right). Kasus yang bisa terjadi:

1. Node tertinggi ada di bagian sub tree kiri dari anak cabang kiri root.

2. Node tertinggi ada di bagian sub tree kanan dari anak cabang kanan root.

Contoh Insertion:

Telah dilakukan insert node dengan value 12 dengan konsep sesuai BST. Kemudian, dilakukan pengecekan terhadap jalur searah hingga ke root, apakah ada tree yang anak cabangnya tidak balance. Ternyata, rootnya memiliki cabang yang tidak balance. Dapat dilihat bahwa anak cabang kiri dari root memiliki tinggi 4 sedangkan anak cabang kanan dari root memiliki tinggi 2. Jika dikurangi (4-2) maka hasilnya adalah 2 dan hal ini telah melanggar ketentuan AVL Tree. Maka dari itu, dilakukan rebalance AVL Tree. Terlihat bahwa garis jalur tidak belok (sub tree kiri pada anak cabang kiri root), maka dilakukan single rotation. Hasilnya menjadi:

Dapat dilihat bahwa telah terjadi single rotation ke kanan karena anak cabang kiri tidak seimbang. Node dengan value 22 berotasi ke kanan menjadi root, kemudian node dengan value 30 akan menjadi anak cabang kanan dari root. Untuk node dengan value 27 akan menjadi anak cabang kiri dari 30.

Contoh Deletion:

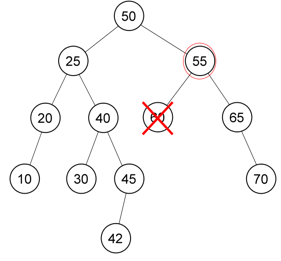
Akan dilakukan deletion pada node dengan value 60. Maka, diambil node dari anak cabang kiri dengan value paling besar. Karena di contoh hanya ada 1 node pada anak cabang kiri, maka node dengan value 55 akan menggantikan posisi node value 60. 

Setelah posisi node berpindah, maka node value 55 menjadi tidak balance karena memiliki 0 anak cabang kiri dan 2 anak cabang kanan (beda 2). Maka dilakukan rotate ke kiri agar kembali seimbang sehingga node value 65 akan menjadi parentnya dan node value 55 akan menjadi anak cabang kiri dari node value 65.

Dilanjutkan kembali pengecekan jalur ke atas yaitu root 50. Ternyata, anak cabang kiri tingginya 4 dan anak cabang kanan tingginya 2 sehingga beda 2 dan melanggar konsep AVL Tree. Karena node yang menjadi penyebab tree tidak seimbang adalah node value 42 dan letaknya sebagai sub tree kanan pada anak cabang kiri root sehingga akan dilakukan double rotation.

Untuk penjelasan lanjutan double rotation, akan dilanjutkan pada section double rotation di bawah.

• Double Rotation

Dilakukan jika anak cabang dari node yang dimasukkan yang tidak balance memiliki jalur yang bengkok dari root (left-right atau right-left). Kasus yang bisa terjadi:

1. Node tertinggi ada di bagian sub tree kanan dari anak cabang kiri root.

2. Node tertinggi ada di bagian sub tree kiri dari anak cabang kanan root.

Contoh Insertion:

Telah dilakukan insert node dengan value 26 dengan konsep sesuai BST. Kemudian, dilakukan pengecekan terhadap jalur searah hingga ke root, apakah ada tree yang anak cabangnya tidak balance. Ternyata, rootnya memiliki cabang yang tidak balance. Dapat dilihat bahwa anak cabang kiri dari root memiliki tinggi 4 sedangkan anak cabang kanan dari root memiliki tinggi 2. Jika dikurangi (4-2) maka hasilnya adalah 2 dan hal ini telah melanggar ketentuan AVL Tree. Maka dari itu, dilakukan rebalance AVL Tree dengan tujuan mengubah sub tree menjadi searah dengan anak cabang kiri root. Terlihat bahwa garis jalur belok (kiri-kanan), maka dilakukan double rotation karena node tertinggi ada di bagian kanan dari anak cabang kiri dari root.

Hasil rotasi pertama menjadi:

Dilakukan rotate ke kiri sehingga node dengan value 27 menjadi parent dan node dengan value 22 berpindah menjadi anak cabang kiri dari node dengan value 27. Untuk cabang node dengan value 24 akan menjadi anak cabang dari node dengan value 22. Dengan begitu, jalur nodenya sudah berada di bagian kiri dari anak cabang kiri root sehingga dapat dilakukan rotation kedua.

Hasil rotasi kedua menjadi:

Dilakukan rotate ke kanan sehingga node dengan value 27 menjadi root dan node dengan value 30 menjadi anak cabang kanan root. Kemudian untuk node dengan value 29 akan menjadi anak cabang dari node dengan value 30. Dengan begitu, tree akan menjadi balance sesuai dengan aturan AVL Tree. Node value 24 memiliki 0 anak cabang kiri dan 1 anak cabang kanan (OK). Node value 22 memiliki anak cabang kiri dan kanan dengan tinggi 2 (OK). Root value 27 memiliki anak cabang kiri dan kanan dengan tinggi 3 (OK).

Contoh Deletion:

Melanjutkan contoh kasus pada deletion di section single rotation di atas. 

Dilanjutkan kembali pengecekan jalur ke atas yaitu root 50. Ternyata, anak cabang kiri tingginya 4 dan anak cabang kanan tingginya 2 sehingga beda 2 dan melanggar konsep AVL Tree. Karena node yang menjadi penyebab tree tidak seimbang adalah node value 42 dan letaknya sebagai sub tree kanan pada anak cabang kiri root sehingga akan dilakukan double rotation.

Pertama, dilakukan rotasi ke kiri supaya sub tree searah dengan anak cabang kiri root. Node value 40 akan menjadi parent dan node value 25 akan menjadi anak cabang kiri dari parent 40. Kemudian anak cabang node value 30 akan menjadi anak cabang kanan dari node value 25.

Kemudian, dilakukan rotasi kedua yaitu rotasi ke kanan agar anak cabang kiri dan kanan root seimbang. Node value 40 akan rotasi ke kanan menjadi root dan node value 50 akan menjadi anak cabang kanan root. Kemudian, node value 45 dan cabangnya akan menjadi anak cabang kiri dari node value 50. Dengan demikian, tree telah balance, dimana anak cabang kiri root dan anak cabang kanan root sama-sama memiliki tinggi 3 dan bedanya (3-3) adalah 0.

Demikian pembahasan dari materi yang saya pelajari. Mohon maaf apabila ada kesalahan dan kekurangan. Terima kasih.

Angelia
2301854492
COMP6048 - CB01

Referensi:
PPT BinusMaya
Penjelasan Pak Ferdinand via Online Video Conference (Zoom)