Heaps and Tries
Angelia
2301854492
COMP6048 - CB01
Pada pertemuan sesi ke-11, dilakukan video conference dengan dosen tamu yang dibawakan oleh
Kak Dwi. Berikut ini rangkuman materi pembahasan mengenai heaps dan tries yang disampaikan dosen tamu.
HEAPS
Heap merupakan pengembangan konsep berdasarkan struktur data Binary Search Tree Complete dengan memenuhi sifat heap.
Konsep heap terdiri dari 3 bentuk:
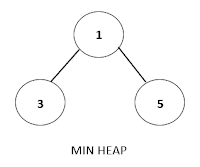
A. Min Heap
IMPLEMENTASI ARRAY DALAM HEAPS
Heap bisa diimplementasikan menggunakan linked list, namun akan jauh lebih mudah jika menggunakan array.
Index array root dimulai dari 1 (bukan 0, dijelaskan di bawah) hingga ke N karena terkait dengan rumus menemukan root.
Cara menggunakan array untuk heaps adalah:
- Index 1 selalu rootnya, dalam contoh ini menggunakan min heap, maka valuenya yang paling kecil, yaitu 7.
- Index berikutnya bergerak maju sejajar mengisi children nodesnya hingga full lalu turun lagi, dst. (Mulai dari kiri ke kanan sampai semua leaf node terisi).
Node yang memiliki relasi dengan parent, left child, dan right child yang menggunakan implementasi array akan lebih mudah diolah.
Cara menemukan index, dengan pemisalahan index node sekarang adalah x:
a. Parent (x) = x/2
b. Left Child (x) = 2 * x
c. Right Child (x) = 2 * x + 1
Misalkan dengan contoh gambar di atas:
Index array [1] = 7, [2] = 15, [4] = 30, [5] = 31
Misalkan current node adalah value 15, ada di index 2.
- Menemukan index parentnya = x/2 = 2/2 = 1, yaitu value 7.
- Menemukan index left child = 2 * x = 2 * 2 = 4, yaitu value 30.
Kenapa value 30 di index 4, karena penyusunan heap sudah pasti mengisi jajaran node hingga full (untuk di height 2 maka harusnya ada 2 node, supaya di height 3 boleh diisi).
- Menemukan index right child = 2 * x + 1 = 2 * 2 + 1 = 5, yaitu value 31.
Dari contoh ilustrasi di atas, maka kita bisa menjawab alasan kenapa root harus index 1. Karena rumus parent(2) = 2/2 = 1 untuk mencapai root dalam kasus contoh di atas. Jika root dimasukkan ke index 0, maka tidak akan akan bisa ditemukan dengan rumus.
MENEMUKAN VALUE TERKECIL DI MIN HEAP
Menemukan value terkecil di min heap sangatlah mudah karena nilai terkecil pasti ada di rootnya yang dimana kita tinggal me-return data[1].
INSERTION DI MIN HEAP
Langkah:
- Memasukkan elemen baru ke node paling bawah kanan yang kosong, atau jika sudah full, masukkan ke child baru paling kiri. (Setelah index dari elemen terakhir).
- Perbaiki struktur dengan konsep upheap terhadap elemen baru tersebut (Memperbaiki sifat heap).
a) Membandingkan current node (mulai dari value node yang baru dimasukkan) dengan value parentnya. Jika value current node lebih kecil dari value parent, maka lakukan swap. Lalu, teruskan upheap parent nodenya.
b) Berhenti jika value current node lebih besar dari value parent atau current nodenya adalah root (tidak ada parent lagi).
Contohnya:
Dimasukkan value baru yaitu 20. Node baru ini diletakkan ke paling bawah kanan setelah index elemen terakhir yaitu sebelah kanan node value 32. Lalu, cek value current node dengan value parent, ternyata 20 < 28, maka swap sehingga posisi parent yang awalnya berisi 28 menjadi 20 dan 28 turun menjadi child dari 20. Lalu, cek lagi ke parentnya yaitu 15, ternyata 20 > 15, maka berhenti.
Contoh lain:
Dimasukkan value baru 5, posisinya paling bawah kanan sebelah value 28. Cek current node dengan parent, ternyata 5 < 17, maka swap, sehingga value di parent yg awalnya 17 menjadi 5 (dan sekarang menjadi current node) dan 17 turun menjadi child.
Lalu, cek lagi current node dengan parent, ternyata 5 < 10, maka swap, sehingga value di parent awalnya 10 menjadi 5 (sekarang jadi current node) dan value 10 menjadi child node dari value 5. Cek lagi ternyaa 5 < 7, maka swap sehingga angka 5 menjadi root (current node) dan sudah paling atas, maka berhenti.
DELETION DI MIN HEAP
Langkah:
- Delete selalu dilakukan paling atas (pada bagian root).
- Replace root dengan elemen terakhir heap.
- Kurangi jumlah elemen heap
- Perbaiki struktur dengan konsep downheap sesuai dengan sifat heap.
a) Bandingkan value current node (mulai dari root) dengan value left child dan right child. Jika ada value child (paling kecil) < current node, maka swap, lalu cek lagi ke bawah.
b) Berhenti jika value current node < value child kiri dan kanan atau current node adalah leaf node. (Tidak memiliki child nodes lagi).
Contohnya:
B. Max Heap
Langkah:
- Memasukkan elemen baru ke node paling bawah kanan yang kosong, atau jika sudah full, masukkan ke child baru paling kiri. (Setelah index dari elemen terakhir).
- Perbaiki struktur dengan konsep upheap terhadap elemen baru tersebut (Memperbaiki sifat heap).
a) Membandingkan current node (mulai dari value node yang baru dimasukkan) dengan value parentnya. Jika value current node lebih besar dari value parent, maka lakukan swap. Lalu, teruskan upheap parent nodenya.
b) Berhenti jika value current node lebih kecil dari value parent atau current nodenya adalah root (tidak ada parent lagi).
DELETION DI MAX HEAP
Langkah:
- Delete selalu dilakukan paling atas (pada bagian root).
- Replace root dengan elemen terakhir heap.
- Kurangi jumlah elemen heap
- Perbaiki struktur dengan konsep downheap sesuai dengan sifat heap.
a) Bandingkan value current node (mulai dari root) dengan value left child dan right child. Jika ada value child (paling besar) > current node, maka swap, lalu cek lagi ke bawah.
b) Berhenti jika value current node > value child kiri dan kanan atau current node adalah leaf node. (Tidak memiliki child nodes lagi).
C. Min-Max Heap
MENEMUKAN VALUE TERBESAR DI MIN_MAX HEAP
Value terbesar pasti berada di children node dari root yaitu pada level 2 antara pada child kiri atau child kanan yang memiliki value terbesar, dengan return max(data[2], data[3]).
#Value terbesar bisa terletak di root jika heap hanya memiliki 1 data.
INSERTION DI MIN-MAX HEAP
Langkah:
- Memasukkan elemen baru ke node paling bawah kanan yang kosong, atau jika sudah full, masukkan ke child baru paling kiri. (Setelah index dari elemen terakhir).
- Perbaiki struktur dengan konsep upheap terhadap elemen baru tersebut (Memperbaiki sifat heap).
a) Jika node baru berada di level min:
* Jika parent < current node, lakukan swap, dan upheapmax dari parentnya.
* Jika parent > current node, lakukan upheapmin dari current node.
b) Jika node baru berada di level max:
* Jika parent > current node, maka lakukan swap, dan upheapmin dari parentnya.
* Jika parent < current node, maka lakukan upheapmax dari current node.
UPHEAPMIN DI MIN-MAX HEAP
Bandingkan value current node dengan value grandparentnya.
Jika value current node < value parent, lakukan swap value, lanjutkan upheapmin grandparent nodenya.
UPHEAPMAX DI MIN-MAX HEAP
Bandingkan value current node dengan value grandparentnya.
Jika value current node > value parent, lakukan swap value, lanjutkan upheapmax grandparent nodenya.
#Intinya, kalau current node maka cek parentnya sesuai kriteria parentnya berada di level tertentu (min/max).
Jika di level min, maka cek apakah value current node lebih kecil dari value parent, jika ya maka swap, jika tidak maka naik lagi ke grandparent (lakukan validasi sesuai min level), dan lakukan hal yang sama secara rekursif hingga ke root.
Jika di level max, maka cek apakah value current node lebih besar dari value parent, jika ya maka swap, jika tidak maka naik lagi ke grandparent (lakukan validasi sesuai maxlevel), lakukan hal yang sama secara rekursif hingga ke root.
CONTOH INSERTION MIN-MAX HEAP
Contoh 1:
Ada insertion value 50, berada di level max. Cek parent dengan current node, ternyata 28 < 50, maka lakukan upheapmax (naik lagi). Cek grandparent, ternyata value grandparent (35) < value current node (50), maka dilakukan swap value dan current node sekarang berada di tempat grandparent.
Lanjut cek parent (min level) dengan current node (max level), 8 < 50, maka cek upheap max namun karena node value 50 tidak memiliki grandparent, maka proses selesai.
Contoh 2:
Ada insertion value 5 di level max. Cek parentnya (14, level min). Ternyata 5 < 14, maka swap valuenya sehingga current node sekarang adalah 5 yang posisinya di parent.
Cek lagi current node (5, min level) dengan parentnya (27, max level). Ternyata 14 < 27, maka cek grandparent (8, min level) dengan current node (5, min level). Ternyata 8 > 5, maka lakukan swap value dan berhenti karena sudah sampai root. Maka hasilnya menjadi:
DELETION DI MIN-MAX HEAP
a) Deletion Value Terkecil
- Replace value root dengan elemen terakhir di heap.
- Mengurangi jumlah elemen di heap.
- Downheapmin dari rootnya.
b) Deletion Value Terbesar
- Mereplace antara anak kiri atau anak kanan dari root (yang nilainya paling besar) dengan elemen terakhir di heap dan akan menjadi current node.
- Kurangi jumlah elemen di heap / hapus index terakhir.
- Downheapmax dari current node
DOWNHEAPMIN DI MIN-MAX HEAP
Misalkan m adalah elemen terkecil di anak current node dan grandchildren (jika ada).
Jika m adalah grandchildren dari current node maka:
- Jika m lebih kecil current node:
* swap valuenya.
* Jika m lebih besar dari parent swap valuenya.
* Lanjutkan downheapmin dari m.
- Jika m adalah anak dari current node maka:
* Jika m lebih kecil dari current node maka swap value.
DOWNHEAPMAX DI MIN-MAX HEAP
Misalkan m adalah elemen terbesar di child current node dan grandchildren (jika ada).
= Jika m adalah grandchildren dari current node maka:
- Jika m lebih besar dari current node:
* swap valuenya.
* Jika m lebih kecil dari parent swap valuenya.
* Lanjutkan downheapmax dari m.
= Jika m adalah anak dari current node maka:
* Jika m lebih besar dari current node maka swap value.
CONTOH DELETION MIN-MAX HEAP
Contoh delete max:
Value paling besar ada di child kiri node yaitu 50, maka ganti 50 dengan elemen terakhir yaitu 14 dan delete leaf node 14. Lalu lakukan downheapmax.
Sekarang current node ada di value 14. Elemen terbesar dari child dan grandchildren adalah 35, yaitu grandchild kanan dari child kanan, maka cek apakah value 35 > 14, maka swap valuenya.
Lalu cek ternyata value grandchild kanan (14) < value parentnya (28), maka swap valuenya. Lanjutkan downheapmax.
Current node sekarang value 28. Karena 28 tidak memiliki children atau grandchildren, maka proses selesai.
APPLICATION OF HEAPSCONCEPT OF TRIES
Tries adalah tree data structure yang sudah terorder yang digunakan untuk menyimpan array asosiatif (biasanya berupa strings). Tries adalah tree dimana tiap vertex mewakili satu kata atau prefix.
Root tries selalu berupa empty character ('') dengan tujuan agar tidak hanya berfokus pada 1 karakter saja. Misalnya jika root dimasukkan huruf 'P', maka hanya bisa membuat kata dengan awalan huruf 'P'.
Penggunaan konsep tries ini bisa ditemukan di aplikasi yang menyimpan data kata (misalnya, daftar kata di KBBI) yang biasa ditemukan pada web browser untuk fitur auto complete text, spell checker untuk mendeteksi tiap huruf dan melakukan koreksi kata, dan masih banyak lagi.
Konsep tries ini dapat memiliki banyak cabang sesuai dengan padanan kata. Contohnya, pada contoh di atas, rootnya adalah empty character. Kemudian ada children node 'B', 'S', dan 'A'.
Dari char 'B' tidak bisa membentuk kata.
Dari char 'S' bisa membentuk kata speak, speaker, spa, space, spaceship, spade.
Dari char 'A' bisa membentuk kata and.
Jika melihat contoh untuk character 'S' maka ada beberapa kata yang tergabung dalam satu susunan, maka pemberian tanda khusus bisa memberi hint batas akhir dari sebuah kata.
SPEAK (PEMBATAS), SPEAKER (PEMBATAS) atau
SPA (PEMBATAS), SPACE (PEMBATAS), SPACESHIP (PEMBATAS) atau SPADE (PEMBATAS).
Referensi:
Zoom Meeting, dosen tamu Kak Dwi
PPT BinusMaya
2301854492
COMP6048 - CB01
Pada pertemuan sesi ke-11, dilakukan video conference dengan dosen tamu yang dibawakan oleh
Kak Dwi. Berikut ini rangkuman materi pembahasan mengenai heaps dan tries yang disampaikan dosen tamu.
HEAPS
Heap merupakan pengembangan konsep berdasarkan struktur data Binary Search Tree Complete dengan memenuhi sifat heap.
Konsep heap terdiri dari 3 bentuk:
A. Min Heap
Konsep min heap adalah bahwa node parent memiliki value paling kecil daripada node childrennya. Hal ini menyimpulkan bahwa value terkecil akan terletak di root tree nya.
IMPLEMENTASI HEAP UNTUK PRIORITY QUEUE
Heap dapat menjadi implementasi priority queue yang efisien.
* mencari minimum = menemukan value terkecil di heap.
* insert/push = insert elemen baru ke dalam heap.
* delete/pop minimum = delete value paling kecil di heap.
IMPLEMENTASI ARRAY DALAM HEAPS
Heap bisa diimplementasikan menggunakan linked list, namun akan jauh lebih mudah jika menggunakan array.
Index array root dimulai dari 1 (bukan 0, dijelaskan di bawah) hingga ke N karena terkait dengan rumus menemukan root.
Cara menggunakan array untuk heaps adalah:
- Index 1 selalu rootnya, dalam contoh ini menggunakan min heap, maka valuenya yang paling kecil, yaitu 7.
- Index berikutnya bergerak maju sejajar mengisi children nodesnya hingga full lalu turun lagi, dst. (Mulai dari kiri ke kanan sampai semua leaf node terisi).
Node yang memiliki relasi dengan parent, left child, dan right child yang menggunakan implementasi array akan lebih mudah diolah.
a. Parent (x) = x/2
b. Left Child (x) = 2 * x
c. Right Child (x) = 2 * x + 1
Misalkan dengan contoh gambar di atas:
Index array [1] = 7, [2] = 15, [4] = 30, [5] = 31
Misalkan current node adalah value 15, ada di index 2.
- Menemukan index parentnya = x/2 = 2/2 = 1, yaitu value 7.
- Menemukan index left child = 2 * x = 2 * 2 = 4, yaitu value 30.
Kenapa value 30 di index 4, karena penyusunan heap sudah pasti mengisi jajaran node hingga full (untuk di height 2 maka harusnya ada 2 node, supaya di height 3 boleh diisi).
- Menemukan index right child = 2 * x + 1 = 2 * 2 + 1 = 5, yaitu value 31.
Dari contoh ilustrasi di atas, maka kita bisa menjawab alasan kenapa root harus index 1. Karena rumus parent(2) = 2/2 = 1 untuk mencapai root dalam kasus contoh di atas. Jika root dimasukkan ke index 0, maka tidak akan akan bisa ditemukan dengan rumus.
MENEMUKAN VALUE TERKECIL DI MIN HEAP
Menemukan value terkecil di min heap sangatlah mudah karena nilai terkecil pasti ada di rootnya yang dimana kita tinggal me-return data[1].
INSERTION DI MIN HEAP
Langkah:
- Memasukkan elemen baru ke node paling bawah kanan yang kosong, atau jika sudah full, masukkan ke child baru paling kiri. (Setelah index dari elemen terakhir).
- Perbaiki struktur dengan konsep upheap terhadap elemen baru tersebut (Memperbaiki sifat heap).
a) Membandingkan current node (mulai dari value node yang baru dimasukkan) dengan value parentnya. Jika value current node lebih kecil dari value parent, maka lakukan swap. Lalu, teruskan upheap parent nodenya.
b) Berhenti jika value current node lebih besar dari value parent atau current nodenya adalah root (tidak ada parent lagi).
Contohnya:
Contoh lain:
DELETION DI MIN HEAP
Langkah:
- Delete selalu dilakukan paling atas (pada bagian root).
- Replace root dengan elemen terakhir heap.
- Kurangi jumlah elemen heap
- Perbaiki struktur dengan konsep downheap sesuai dengan sifat heap.
a) Bandingkan value current node (mulai dari root) dengan value left child dan right child. Jika ada value child (paling kecil) < current node, maka swap, lalu cek lagi ke bawah.
b) Berhenti jika value current node < value child kiri dan kanan atau current node adalah leaf node. (Tidak memiliki child nodes lagi).
Contohnya:
Dilakukan deletion pertama yaitu value 7 yang ada di root. Maka ganti value root dengan value node paling kanan bawah atau node elemen paling terakhir, yaitu 28. Maka value root sekarang adalah 28, dan node elemen terakhir bisa dihapus. Kemudian, cek anak kiri dan kanan, ternyata value paling kecil ada di child kanan (10<15<28), maka swap value root dengan value child kanan sehingga current node sekarang di child kanan dengan value 28.
Lanjut cek ke bawah, antara current node dengan left dan right child, ternyata RC (12) < LF (17) < P (28), maka swap right child dengan parent sehingga value right child sekarang menjadi 28 dan parentnya menjadi 12. Ketika hendak dilanjut cek ke bawah, ternyata node value 28 sudah merupakan leaf node, sehingga berhenti.
B. Max Heap
Konsep max heap adalah bahwa node parent memiliki value paling besar daripada node childrennya.
Jadi, value terbesar berada di root heapnya.
IMPLEMENTASI HEAP UNTUK PRIORITY QUEUE
Heap dapat menjadi implementasi priority queue yang efisien.
* mencari max= menemukan value terbesar di heap.
* insert/push = insert elemen baru ke dalam heap.
* delete/pop max= delete value paling besar di heap.
Prinsip insertion dan deletion mirip dengan min heap.
INSERTION DI MAX HEAPLangkah:
- Memasukkan elemen baru ke node paling bawah kanan yang kosong, atau jika sudah full, masukkan ke child baru paling kiri. (Setelah index dari elemen terakhir).
- Perbaiki struktur dengan konsep upheap terhadap elemen baru tersebut (Memperbaiki sifat heap).
a) Membandingkan current node (mulai dari value node yang baru dimasukkan) dengan value parentnya. Jika value current node lebih besar dari value parent, maka lakukan swap. Lalu, teruskan upheap parent nodenya.
b) Berhenti jika value current node lebih kecil dari value parent atau current nodenya adalah root (tidak ada parent lagi).
DELETION DI MAX HEAP
Langkah:
- Delete selalu dilakukan paling atas (pada bagian root).
- Replace root dengan elemen terakhir heap.
- Kurangi jumlah elemen heap
- Perbaiki struktur dengan konsep downheap sesuai dengan sifat heap.
a) Bandingkan value current node (mulai dari root) dengan value left child dan right child. Jika ada value child (paling besar) > current node, maka swap, lalu cek lagi ke bawah.
b) Berhenti jika value current node > value child kiri dan kanan atau current node adalah leaf node. (Tidak memiliki child nodes lagi).
C. Min-Max Heap
Konsep min-max heap adalah bahwa untuk height awal pasti menggunakan konsep min heap dimana node valuenya paling kecil dibanding childrennya, lalu di height ke-2 menggunakan konsep max heap dimana value node paling besar dibanding childrennya, dan berlanjut terus menggunakan konsep heap secara bergantian.
Kondisi heap pada bentuk ini memiliki 2 bentuk antara minimum dan maximum.
- Tiap elemen di level ganjil/genap lebih kecil dari semua anaknya (min level).
- Tiap elemen di level ganjil/genap lebih besar dari semua anaknya (max level).
Tujuan min-max heap adalah untuk mempermudah kita mencari nilai terkecil dan terbesar dalam heap di waktu yang bersamaan.
MENEMUKAN VALUE TERKECIL DI MIN-MAX HEAP
Value terkecil di heap pasti berada di level 0 atau di root, dengan return data[1].
Value terbesar pasti berada di children node dari root yaitu pada level 2 antara pada child kiri atau child kanan yang memiliki value terbesar, dengan return max(data[2], data[3]).
#Value terbesar bisa terletak di root jika heap hanya memiliki 1 data.
INSERTION DI MIN-MAX HEAP
Langkah:
- Memasukkan elemen baru ke node paling bawah kanan yang kosong, atau jika sudah full, masukkan ke child baru paling kiri. (Setelah index dari elemen terakhir).
- Perbaiki struktur dengan konsep upheap terhadap elemen baru tersebut (Memperbaiki sifat heap).
a) Jika node baru berada di level min:
* Jika parent < current node, lakukan swap, dan upheapmax dari parentnya.
* Jika parent > current node, lakukan upheapmin dari current node.
b) Jika node baru berada di level max:
* Jika parent > current node, maka lakukan swap, dan upheapmin dari parentnya.
* Jika parent < current node, maka lakukan upheapmax dari current node.
UPHEAPMIN DI MIN-MAX HEAP
Bandingkan value current node dengan value grandparentnya.
Jika value current node < value parent, lakukan swap value, lanjutkan upheapmin grandparent nodenya.
UPHEAPMAX DI MIN-MAX HEAP
Bandingkan value current node dengan value grandparentnya.
Jika value current node > value parent, lakukan swap value, lanjutkan upheapmax grandparent nodenya.
#Intinya, kalau current node maka cek parentnya sesuai kriteria parentnya berada di level tertentu (min/max).
Jika di level min, maka cek apakah value current node lebih kecil dari value parent, jika ya maka swap, jika tidak maka naik lagi ke grandparent (lakukan validasi sesuai min level), dan lakukan hal yang sama secara rekursif hingga ke root.
Jika di level max, maka cek apakah value current node lebih besar dari value parent, jika ya maka swap, jika tidak maka naik lagi ke grandparent (lakukan validasi sesuai maxlevel), lakukan hal yang sama secara rekursif hingga ke root.
CONTOH INSERTION MIN-MAX HEAP
Contoh 1:
Contoh 2:
DELETION DI MIN-MAX HEAP
a) Deletion Value Terkecil
- Replace value root dengan elemen terakhir di heap.
- Mengurangi jumlah elemen di heap.
- Downheapmin dari rootnya.
b) Deletion Value Terbesar
- Mereplace antara anak kiri atau anak kanan dari root (yang nilainya paling besar) dengan elemen terakhir di heap dan akan menjadi current node.
- Kurangi jumlah elemen di heap / hapus index terakhir.
- Downheapmax dari current node
DOWNHEAPMIN DI MIN-MAX HEAP
Misalkan m adalah elemen terkecil di anak current node dan grandchildren (jika ada).
Jika m adalah grandchildren dari current node maka:
- Jika m lebih kecil current node:
* swap valuenya.
* Jika m lebih besar dari parent swap valuenya.
* Lanjutkan downheapmin dari m.
- Jika m adalah anak dari current node maka:
* Jika m lebih kecil dari current node maka swap value.
DOWNHEAPMAX DI MIN-MAX HEAP
Misalkan m adalah elemen terbesar di child current node dan grandchildren (jika ada).
= Jika m adalah grandchildren dari current node maka:
- Jika m lebih besar dari current node:
* swap valuenya.
* Jika m lebih kecil dari parent swap valuenya.
* Lanjutkan downheapmax dari m.
= Jika m adalah anak dari current node maka:
* Jika m lebih besar dari current node maka swap value.
CONTOH DELETION MIN-MAX HEAP
Contoh delete max:
APPLICATION OF HEAPSCONCEPT OF TRIES
Tries adalah tree data structure yang sudah terorder yang digunakan untuk menyimpan array asosiatif (biasanya berupa strings). Tries adalah tree dimana tiap vertex mewakili satu kata atau prefix.
Root tries selalu berupa empty character ('') dengan tujuan agar tidak hanya berfokus pada 1 karakter saja. Misalnya jika root dimasukkan huruf 'P', maka hanya bisa membuat kata dengan awalan huruf 'P'.
Penggunaan konsep tries ini bisa ditemukan di aplikasi yang menyimpan data kata (misalnya, daftar kata di KBBI) yang biasa ditemukan pada web browser untuk fitur auto complete text, spell checker untuk mendeteksi tiap huruf dan melakukan koreksi kata, dan masih banyak lagi.
Konsep tries ini dapat memiliki banyak cabang sesuai dengan padanan kata. Contohnya, pada contoh di atas, rootnya adalah empty character. Kemudian ada children node 'B', 'S', dan 'A'.
Dari char 'B' tidak bisa membentuk kata.
Dari char 'S' bisa membentuk kata speak, speaker, spa, space, spaceship, spade.
Dari char 'A' bisa membentuk kata and.
Jika melihat contoh untuk character 'S' maka ada beberapa kata yang tergabung dalam satu susunan, maka pemberian tanda khusus bisa memberi hint batas akhir dari sebuah kata.
SPEAK (PEMBATAS), SPEAKER (PEMBATAS) atau
SPA (PEMBATAS), SPACE (PEMBATAS), SPACESHIP (PEMBATAS) atau SPADE (PEMBATAS).
Demikian pembahasan dari materi yang saya pelajari. Mohon maaf apabila ada kesalahan dan kekurangan. Terima kasih.
Angelia
2301854492
COMP6048 - CB01
2301854492
COMP6048 - CB01
Referensi:
Zoom Meeting, dosen tamu Kak Dwi
PPT BinusMaya
Comments
Post a Comment