Rangkuman Semua Materi Data Structure
2301854492
Hari: Senin, 15/06/2020
Kelas: CB01
Lecturer:
- Henry Chong (D4460)
- Ferdinand Ariandy Luwinda (D4522)
Single Linked List merupakan kumpulan data yang terhubung dengan 1 pointer, yaitu pointer yang merujuk ke data setelahnya. (Penjelasan lebih lengkap ada pada Double Linked List, karena materi DLL lebih dulu dibuat).
2. Implementasi Single Linked List
Dokumentasi hasil code di lab:
#include<stdio.h>
#include<stdlib.h>
struct Data{
int value;
Data *next;
}*head = NULL, *tail = NULL, *current;
int value;
void inputNilai(){
printf("Masukkan Nilai \t: ");
scanf("%d", &value);
getchar();
}
void pushDepan(int value){
current = (struct Data*) malloc(sizeof(Data));
current->value = value;
current->next = NULL;
if(head == NULL){
head = tail = current;
}
else{
current->next = head;
head = current;
}
}
void pushBelakang(int value){
current = (struct Data*) malloc(sizeof(Data));
current->value = value;
current->next = NULL;
if(head == NULL){
head = tail = current;
}
else{
tail->next = current;
tail = current;
}
}
void pushMid(int value){
//No Data
if(head == NULL) pushDepan(value);
else if(value < head->value) pushDepan(value);
else if(value > tail->value) pushBelakang(value);
else{
current = (struct Data*) malloc(sizeof(Data));
current->value = value;
current->next = NULL;
Data *temp = head;
while(temp->next->value < value){
temp = temp->next;
}
current->next = temp->next;
temp->next = current;
}
}
void popDepan(){
//No Data
if(head == NULL) printf("Pop Failed!\nNo Data!\n");
else{
current = head;
if(head == tail){
//Data = 1
free(current);
head = tail = NULL;
}
else{
//Data > 1
head = head->next;
free(current);
}
}
}
void popBelakang(){
//No Data
if(head == NULL) printf("Pop Failed!\nNo Data!\n");
else{
current = head;
if(head == tail){
//Data = 1
free(current);
head = tail = NULL;
}
else{
//Data > 1
while(current->next != tail){
current = current->next;
}
free(tail);
tail = current;
tail->next = NULL;
}
}
}
void popMid(int value){
if(head == NULL) printf("Pop Failed!\nNo Data!\n");
else if(value == head->value) popDepan();
else if(value == tail->value) popBelakang();
else{
current = head;
Data *temp = head;
while(current != NULL && current->value != value){
temp = current;
current = current->next;
}
if(current == NULL) printf("Pop(%d) Failed!\n%d is not found!\n", value, value);
else{
temp->next = current->next;
free(current);
printf("Data %d Deleted!\n", value);
}
}
}
void cetak(){
current = head;
while(current != NULL){
printf("%d\n", current->value);
current = current->next;
}
}
int main(){
int choose = -1;
do{
printf("===== SINGLE LINKED LIST MENU =====\n");
printf("1. Add Data (Front)\n");
printf("2. Add Data (End)\n");
printf("3. Add Data Mid [Sorted Data]\n");
printf("4. Delete First Data\n");
printf("5. Delete Last Data\n");
printf("6. Delete Targeted Data [Sorted Data]\n");
printf("7. View Data\n");
printf("8. Exit\n");
printf("Choose >> ");
scanf("%d", &choose);
getchar();
switch(choose){
case 1:
inputNilai();
pushDepan(value);
printf("Insert Front Data Success!\n");
break;
case 2:
inputNilai();
pushBelakang(value);
printf("Insert Back Data Success!\n");
break;
case 3:
inputNilai();
pushMid(value);
printf("Insert Mid Data Success!\n");
break;
case 4:
popDepan();
printf("First Data Deleted!\n");
break;
case 5:
popBelakang();
printf("Last Data Deleted!\n");
break;
case 6:
inputNilai();
popMid(value);
break;
case 7:
cetak();
break;
case 8:
printf("Anda keluar aplikasi");
break;
}
printf("\nPress ENTER to continue...");
getchar();
}
while(choose != 8);
}
Double Linked List merupakan kumpulan data yang terhubung dengan 2 pointer, satu pointer merujuk pada data setelahnya dan satu pointer merujuk pada data sebelumnya.
2. Perbedaan 'Double Linked List' dengan 'Single Linked List'
Tak jauh berbeda dengan materi single linked list, double linked list memiliki konsep yang sama. Sebagai ilustrasi, single linked list hanya dapat berpegangan menggunakan tangan kanan saja (arah akses pointer hanya ke kanan saja, 1 pointer penunjuk), sedangkan double linked list dapat berpegangan menggunakan tangan kiri dan kanan (arah akses pointer dapat ke kiri dan ke kanan, 2 pointer penunjuk).
3. Model Double Linked List
* Default Linked List
Model Linked List ini (Double Linked List) dapat mengakses data sebelum dan sesudahnya, namun jika node berada di bagian akhir/awal data, salah satu pointernya tidak dapat mengakses data selanjutnya atau sebelumnya.
Penjelasan:
Sumber: Geeksforgeeks.org
Berdasarkan contoh gambar di atas, jika node berada di value data 'A' maka pointer ke kiri (kembali ke data paling akhir) untuk mengakses value data 'D' tidak ada/tidak bisa. Begitu pula dengan kondisi jika node berada di value data 'D' maka pointer ke kanan (kembali ke data paling awal) untuk mengakses value data 'A' tidak ada/tidak bisa.
* Circular Linked List
Model Linked List ini dapat mengakses data sebelum dan sesudahnya, serta model Circular ini dapat mengakses data paling awal saat node berada pada data paling akhir dan dapat mengakses data paling akhir saat node berada pada data paling awal.
Penjelasan:
Sumber: Geeksforgeeks.org
Berdasarkan contoh gambar di atas, ketika node berada pada data paling awal (katakanlah Data 'A') maka model ini memiliki fitur untuk mengakses data paling akhir (katakanlah Data 'C'). Begitu pula sebaliknya, ketika posisi node berada di Data 'C', maka dapat mengakses data yang posisinya berada paling awal (Data 'A').
Perbedaan model ini dengan model yang biasanya adalah pada fitur yaitu jika posisi node berada di bagian paling awal/akhir data, maka node tersebut dapat pula mengakses posisi data yang berada di bagian paling akhir/awal data tersebut (lawan ujung dari posisi node).
Tambahan:
Model ini juga diterapkan untuk 'Circular Single Linked List'.
Sumber: javatpoint.com
Perbedaan 'Circular Double Linked List' dengan 'Circular Single Linked List' hanya terletak pada pengizinan akses pointernya saja, dimana untuk Circular Double Linked List memiliki 2 pointer penunjuk (bisa mengakses data sebelum dan sesudahnya) sedangkan untuk Circular Single Linked List hanya memiliki 1 pointer penunjuk (hanya bisa mengakses data selanjutnya saja). Untuk fitur model 'Circular'nya sendiri memiliki fungsionalitas yang sama, yaitu agar dapat mengakses data yang posisinya berada di bagian paling awal/akhir ketika node berada di posisi paling akhir/awal (ujung yang berlawanan).
4. Implementasi Penggunaan Double Linked List
Dokumentasi hasil code di lab
#include<stdio.h>
#include<stdlib.h>
struct Data{
int value;
Data *next, *prev;
}*head = NULL, *tail = NULL, *current;
int value;
void inputNilai(){
printf("Masukkan Nilai \t: ");
scanf("%d", &value);
getchar();
}
void pushDepan(int value){
current = (struct Data*) malloc(sizeof(Data));
current->value = value;
current->next = NULL;
current->prev = NULL;
if(head == NULL){
head = tail = current;
}
else{
current->next = head;
head->prev = current;
head = current;
}
}
void pushBelakang(int value){
current = (struct Data*) malloc(sizeof(Data));
current->value = value;
current->next = NULL;
current->prev = NULL;
if(head == NULL){
head = tail = current;
}
else{
tail->next = current;
current->prev = tail;
tail = current;
}
}
void pushMid(int value){
//No Data
if(head == NULL) pushDepan(value);
else if(value < head->value) pushDepan(value);
else if(value > tail->value) pushBelakang(value);
else{
current = (struct Data*) malloc(sizeof(Data));
current->value = value;
current->next = NULL;
current->prev = NULL;
Data *temp = head;
while(temp->next->value < value){
temp = temp->next;
}
current->next = temp->next;
current->prev = temp;
temp->next->prev = current;
temp->next = current;
}
}
void popDepan(){
//No Data
if(head == NULL) printf("Pop Failed!\nNo Data!\n");
else{
current = head;
if(head == tail){
//Data = 1
free(current);
head = tail = NULL;
}
else{
//Data > 1
head = head->next;
free(current);
head->prev = NULL;
}
}
}
void popBelakang(){
//No Data
if(head == NULL) printf("Pop Failed!\nNo Data!\n");
else{
current = tail;
if(head == tail){
//Data = 1
free(current);
head = tail = NULL;
}
else{
//Data > 1
tail = current->prev;
free(current);
tail->next = NULL;
}
}
}
void popMid(int value){
if(head == NULL) printf("Pop Failed!\nNo Data!\n");
else if(value == head->value) popDepan();
else if(value == tail->value) popBelakang();
else{
current = head;
while(current != NULL && current->value != value){
current = current->next;
}
if(current == NULL) printf("Pop(%d) Failed!\n%d is not found!\n", value, value);
else{
current->prev->next = current->next;
current->next->prev = current->prev;
free(current);
printf("Data %d Deleted!\n", value);
}
}
}
void cetak(){
current = head;
while(current != NULL){
printf("%d\n", current->value);
current = current->next;
}
}
int main(){
int choose = -1;
do{
printf("===== DOUBLE LINKED LIST MENU =====\n");
printf("1. Add Data Mid [Sorted Data]\n");
printf("2. Delete Targeted Data [Sorted Data]\n");
printf("3. View Data\n");
printf("4. Exit\n");
printf("Choose >> ");
scanf("%d", &choose);
getchar();
switch(choose){
case 1:
inputNilai();
pushMid(value);
printf("Insert Mid Data Success!\n");
break;
case 2:
inputNilai();
popMid(value);
break;
case 3:
cetak();
break;
case 4:
printf("Anda keluar aplikasi");
break;
}
printf("\nPress ENTER to continue...");
getchar();
}
while(choose != 4);
}
#include <stdlib.h>
struct node{
int value;
struct node *next, *prev;
} *head = NULL, *tail = NULL, *curr;
void push_mid(int x){
curr = (struct node*)malloc(sizeof(struct node));
curr->value = x;
curr->next = curr->prev = NULL;
if(head == NULL){
head = tail = curr;
}
else if (x < head->value){
//push head
curr->next = head;
head->prev = curr;
head = curr;
}
else if (x > tail->value){
//push tail
tail->next = curr;
curr->prev = tail;
tail = curr;
}
else{
node* temp = head;
while(temp->next->value < x){
temp = temp->next;
}
curr->next = temp->next;
temp->next->prev = curr;
temp->next = curr;
curr->prev = temp;
}
}
void pop(int x){
if (head == NULL){
puts("Pop(x) failed! No Data in LL");
}
else if(head == tail){
//only 1 data
free(head);
head = tail = NULL;
}
else if(x == head->value){
//data located at head
curr = head;
head = head->next;
free(curr);
head->prev = NULL;
}
else if(x == tail->value){
//data located at tail
curr = tail;
tail = tail->prev;
free(curr);
tail->next = NULL;
}
else{
curr = head;
while(curr != NULL && curr->value != x){
curr = curr->next;
}
if(curr == NULL){
puts("Pop(x) failed. x is not found!");
}
else{
curr->next->prev = curr->prev;
curr->prev->next = curr->next;
free(curr);
}
}
}
void print_all(){
curr = head; //point to first data
while( curr != NULL )
{
printf("%d ",curr->value);
curr = curr->next;
}
}
int main()
{
push_mid(15);
push_mid(50);
push_mid(99);
push_mid(20);
push_mid(30);
push_mid(25);
push_mid(100);
pop(200);
pop(50);
pop(15);
pop(100);
pop(30);
push_mid(200);
print_all();
return 0;
}
1. Stack
Konsep stack mirip seperti LIFO (Last In First Out). Jadi, data paling akhir yang masuk, data itu yang akan dikeluarkan terlebih dahulu. Pemisalan konsep seperti penumpukkan buku, dimana buku paling atas yaitu buku yang paling terakhir dimasukkan yang akan dikeluarkan terlebih dahulu.
Jenis Linked List yang digunakan: pushDepan dan popDepan, pushBelakang dan popBelakang.
Implementasi Stack: Konversi Infix ke Prefix atau Postfix.
2. Queue
Konsep queue mirip seperti FIFO (First In First Out). Jadi, data yang paling awal masuk, data itulah yang akan dikeluarkan terlebih dahulu. Pemahaman konsep termudah adalah seperti kegiatan mengantri, dimana orang paling depan akan keluar terlebih dahulu.
Pengertian Hashing
Jadi, hashing merupakan teknik yang digunakan untuk mengubah string dengan panjang yang asli menjadi lebih pendek.
Teknik hashing ini biasa digunakan untuk mengambil suatu item dari database. Teknik ini dipilih karena item bisa ditemukan lebih cepat dengan menggunakan kunci hash daripada menggunakan nilai asli.
Hashing juga merupakan konsep mendistribusikan kunci dalam array (table hash) menggunakan fungsi hash.
Sumber: https://en.wikipedia.org/wiki/Hash_function
Pengertian Hash Table
Hash table menjadi tempat penyimpanan string sementara.
Index tabel adalah kunci hashnya, kemudian value tabel adalah string aslinya.
Ukuran hash table bisa lebih sedikit dibandingkan jumlah string asli yang ada, karena beberapa string dapat memiliki kunci hash yang sama.
Contoh Konsep Hash
Soal:
Menyimpan 5 string: define, atan, char, float, exp dengan fungsi hash "ubah karakter dari tiap string menjadi angka mulai dari 0...25"
Dari soal tersebut, maka dapat diklasifikasikan:
a) Index tabel adalah angka 0...25
b) Fungsi hash adalah "ubah karakter dari tiap string menjadi angka mulai dari 0...25"
c) Value tabel adalah define, atan, char, float, exp
Maka, dari penjabaran di atas, dapat disesuaikan bahwa
indeks 0 diisi dengan string atan karena awal karakternya 'a'.
indeks 1 kosong karena tidak ada string yang awal karakternya 'b'.
indeks 2 diisi dengan string char karena awal karakternya 'c'.
indeks 3 diisi dengan string define karena awal karakternya 'd'.
indeks 4 diisi dengan string exp karena awal karakternya 'e'.
indeks 5 diisi dengan string float karena awal karakternya 'f'.
dst
Dari, pengelompokkan di atas, maka didapat hash table sebagai berikut:
void linearProbing(int key, char name[]){
if(strcmp(data[key],"") == 0 ){
strcpy(data[key],name);
}else{
for(i=key+1; i<TABLE_SIZE ; i++ ){
if(i == key){
printf("Failed to insert %s because TABLE is FULL\n",name);
break;
}
if(strcmp(data[i],"") == 0 ){
strcpy(data[i],name);
break;
}
if (i == TABLE_SIZE -1) i = -1;
}
}
}
void print(){
for(i = 0;i<TABLE_SIZE;i++){
printf("%d. %s\n",i,data[i]);
}
}
A. Pengertian Binary Search Tree
Binary Search Tree atau biasa disingkat BST merupakan salah satu struktur data yang mempercepat pencarian dan pengurutan (sorting), dengan metode insertion dan deletion yang mudah. BST dikenal juga sebagai binary tree yang diurutkan (sorted version of Binary Tree).
B. Properti Binary Tree
Berikut ini penjelasan properti di Binary Search Tree:
Sumber: Geeksforgeeks.org
Menggunakan contoh dari gambar di atas, maka akan dijelaskan macam-macam istilah dalam BST:
- Root : Berperan sebagai akar paling atas/pusatnya tree, yaitu angka 8.
- Parent : Node yang berada satu level di atas suatu node tertentu, contohnya angka 3 adalah parent node dari angka 1 dan angka 6.
- Child : Node yang berada satu level di bawah suatu node tertentu, contohnya angka 14 adalah child node dari angka 10.
- Leaf : Node yang tidak memiliki child, contohnya angka 1, 4, 7, dan 13.
- Sibling : Node yang memiliki parent yang sama, contohnya angka 1 dan angka 6.
C. Konsep Binary Search Tree
Binary Tree memiliki akar atau yang disebut root node dan memiliki 2 sisi cabang tree yaitu tree cabang kiri dan tree cabang kanan.
Tree cabang kiri akan selalu menampung value yang lebih kecil dari value parentnya, sedangkan
tree cabang kanan akan selalu menampung value yang lebih besar dari value parentnya.
Binary Tree memiliki syarat yaitu batas maksimum anak dari node parent adalah 2 child nodes.
Simulasi alur penempatan value di BST (dengan root angka '8' dan inputan angka '4':
- Ferdinand Ariandy Luwinda (D4522)
UTS
SINGLE LINKED LIST
1. Pengertian Single Linked ListSingle Linked List merupakan kumpulan data yang terhubung dengan 1 pointer, yaitu pointer yang merujuk ke data setelahnya. (Penjelasan lebih lengkap ada pada Double Linked List, karena materi DLL lebih dulu dibuat).
2. Implementasi Single Linked List
Dokumentasi hasil code di lab:
#include<stdio.h>
#include<stdlib.h>
struct Data{
int value;
Data *next;
}*head = NULL, *tail = NULL, *current;
int value;
void inputNilai(){
printf("Masukkan Nilai \t: ");
scanf("%d", &value);
getchar();
}
void pushDepan(int value){
current = (struct Data*) malloc(sizeof(Data));
current->value = value;
current->next = NULL;
if(head == NULL){
head = tail = current;
}
else{
current->next = head;
head = current;
}
}
void pushBelakang(int value){
current = (struct Data*) malloc(sizeof(Data));
current->value = value;
current->next = NULL;
if(head == NULL){
head = tail = current;
}
else{
tail->next = current;
tail = current;
}
}
void pushMid(int value){
//No Data
if(head == NULL) pushDepan(value);
else if(value < head->value) pushDepan(value);
else if(value > tail->value) pushBelakang(value);
else{
current = (struct Data*) malloc(sizeof(Data));
current->value = value;
current->next = NULL;
Data *temp = head;
while(temp->next->value < value){
temp = temp->next;
}
current->next = temp->next;
temp->next = current;
}
}
void popDepan(){
//No Data
if(head == NULL) printf("Pop Failed!\nNo Data!\n");
else{
current = head;
if(head == tail){
//Data = 1
free(current);
head = tail = NULL;
}
else{
//Data > 1
head = head->next;
free(current);
}
}
}
void popBelakang(){
//No Data
if(head == NULL) printf("Pop Failed!\nNo Data!\n");
else{
current = head;
if(head == tail){
//Data = 1
free(current);
head = tail = NULL;
}
else{
//Data > 1
while(current->next != tail){
current = current->next;
}
free(tail);
tail = current;
tail->next = NULL;
}
}
}
void popMid(int value){
if(head == NULL) printf("Pop Failed!\nNo Data!\n");
else if(value == head->value) popDepan();
else if(value == tail->value) popBelakang();
else{
current = head;
Data *temp = head;
while(current != NULL && current->value != value){
temp = current;
current = current->next;
}
if(current == NULL) printf("Pop(%d) Failed!\n%d is not found!\n", value, value);
else{
temp->next = current->next;
free(current);
printf("Data %d Deleted!\n", value);
}
}
}
void cetak(){
current = head;
while(current != NULL){
printf("%d\n", current->value);
current = current->next;
}
}
int main(){
int choose = -1;
do{
printf("===== SINGLE LINKED LIST MENU =====\n");
printf("1. Add Data (Front)\n");
printf("2. Add Data (End)\n");
printf("3. Add Data Mid [Sorted Data]\n");
printf("4. Delete First Data\n");
printf("5. Delete Last Data\n");
printf("6. Delete Targeted Data [Sorted Data]\n");
printf("7. View Data\n");
printf("8. Exit\n");
printf("Choose >> ");
scanf("%d", &choose);
getchar();
switch(choose){
case 1:
inputNilai();
pushDepan(value);
printf("Insert Front Data Success!\n");
break;
case 2:
inputNilai();
pushBelakang(value);
printf("Insert Back Data Success!\n");
break;
case 3:
inputNilai();
pushMid(value);
printf("Insert Mid Data Success!\n");
break;
case 4:
popDepan();
printf("First Data Deleted!\n");
break;
case 5:
popBelakang();
printf("Last Data Deleted!\n");
break;
case 6:
inputNilai();
popMid(value);
break;
case 7:
cetak();
break;
case 8:
printf("Anda keluar aplikasi");
break;
}
printf("\nPress ENTER to continue...");
getchar();
}
while(choose != 8);
}
DOUBLE LINKED LIST
1. Pengertian Double Linked ListDouble Linked List merupakan kumpulan data yang terhubung dengan 2 pointer, satu pointer merujuk pada data setelahnya dan satu pointer merujuk pada data sebelumnya.
2. Perbedaan 'Double Linked List' dengan 'Single Linked List'
Tak jauh berbeda dengan materi single linked list, double linked list memiliki konsep yang sama. Sebagai ilustrasi, single linked list hanya dapat berpegangan menggunakan tangan kanan saja (arah akses pointer hanya ke kanan saja, 1 pointer penunjuk), sedangkan double linked list dapat berpegangan menggunakan tangan kiri dan kanan (arah akses pointer dapat ke kiri dan ke kanan, 2 pointer penunjuk).
3. Model Double Linked List
* Default Linked List
Model Linked List ini (Double Linked List) dapat mengakses data sebelum dan sesudahnya, namun jika node berada di bagian akhir/awal data, salah satu pointernya tidak dapat mengakses data selanjutnya atau sebelumnya.
Penjelasan:
Berdasarkan contoh gambar di atas, jika node berada di value data 'A' maka pointer ke kiri (kembali ke data paling akhir) untuk mengakses value data 'D' tidak ada/tidak bisa. Begitu pula dengan kondisi jika node berada di value data 'D' maka pointer ke kanan (kembali ke data paling awal) untuk mengakses value data 'A' tidak ada/tidak bisa.
* Circular Linked List
Model Linked List ini dapat mengakses data sebelum dan sesudahnya, serta model Circular ini dapat mengakses data paling awal saat node berada pada data paling akhir dan dapat mengakses data paling akhir saat node berada pada data paling awal.
Penjelasan:
Berdasarkan contoh gambar di atas, ketika node berada pada data paling awal (katakanlah Data 'A') maka model ini memiliki fitur untuk mengakses data paling akhir (katakanlah Data 'C'). Begitu pula sebaliknya, ketika posisi node berada di Data 'C', maka dapat mengakses data yang posisinya berada paling awal (Data 'A').
Perbedaan model ini dengan model yang biasanya adalah pada fitur yaitu jika posisi node berada di bagian paling awal/akhir data, maka node tersebut dapat pula mengakses posisi data yang berada di bagian paling akhir/awal data tersebut (lawan ujung dari posisi node).
Tambahan:
Model ini juga diterapkan untuk 'Circular Single Linked List'.
Perbedaan 'Circular Double Linked List' dengan 'Circular Single Linked List' hanya terletak pada pengizinan akses pointernya saja, dimana untuk Circular Double Linked List memiliki 2 pointer penunjuk (bisa mengakses data sebelum dan sesudahnya) sedangkan untuk Circular Single Linked List hanya memiliki 1 pointer penunjuk (hanya bisa mengakses data selanjutnya saja). Untuk fitur model 'Circular'nya sendiri memiliki fungsionalitas yang sama, yaitu agar dapat mengakses data yang posisinya berada di bagian paling awal/akhir ketika node berada di posisi paling akhir/awal (ujung yang berlawanan).
4. Implementasi Penggunaan Double Linked List
Dokumentasi hasil code di lab
#include<stdio.h>
#include<stdlib.h>
struct Data{
int value;
Data *next, *prev;
}*head = NULL, *tail = NULL, *current;
int value;
void inputNilai(){
printf("Masukkan Nilai \t: ");
scanf("%d", &value);
getchar();
}
void pushDepan(int value){
current = (struct Data*) malloc(sizeof(Data));
current->value = value;
current->next = NULL;
current->prev = NULL;
if(head == NULL){
head = tail = current;
}
else{
current->next = head;
head->prev = current;
head = current;
}
}
void pushBelakang(int value){
current = (struct Data*) malloc(sizeof(Data));
current->value = value;
current->next = NULL;
current->prev = NULL;
if(head == NULL){
head = tail = current;
}
else{
tail->next = current;
current->prev = tail;
tail = current;
}
}
void pushMid(int value){
//No Data
if(head == NULL) pushDepan(value);
else if(value < head->value) pushDepan(value);
else if(value > tail->value) pushBelakang(value);
else{
current = (struct Data*) malloc(sizeof(Data));
current->value = value;
current->next = NULL;
current->prev = NULL;
Data *temp = head;
while(temp->next->value < value){
temp = temp->next;
}
current->next = temp->next;
current->prev = temp;
temp->next->prev = current;
temp->next = current;
}
}
void popDepan(){
//No Data
if(head == NULL) printf("Pop Failed!\nNo Data!\n");
else{
current = head;
if(head == tail){
//Data = 1
free(current);
head = tail = NULL;
}
else{
//Data > 1
head = head->next;
free(current);
head->prev = NULL;
}
}
}
void popBelakang(){
//No Data
if(head == NULL) printf("Pop Failed!\nNo Data!\n");
else{
current = tail;
if(head == tail){
//Data = 1
free(current);
head = tail = NULL;
}
else{
//Data > 1
tail = current->prev;
free(current);
tail->next = NULL;
}
}
}
void popMid(int value){
if(head == NULL) printf("Pop Failed!\nNo Data!\n");
else if(value == head->value) popDepan();
else if(value == tail->value) popBelakang();
else{
current = head;
while(current != NULL && current->value != value){
current = current->next;
}
if(current == NULL) printf("Pop(%d) Failed!\n%d is not found!\n", value, value);
else{
current->prev->next = current->next;
current->next->prev = current->prev;
free(current);
printf("Data %d Deleted!\n", value);
}
}
}
void cetak(){
current = head;
while(current != NULL){
printf("%d\n", current->value);
current = current->next;
}
}
int main(){
int choose = -1;
do{
printf("===== DOUBLE LINKED LIST MENU =====\n");
printf("1. Add Data Mid [Sorted Data]\n");
printf("2. Delete Targeted Data [Sorted Data]\n");
printf("3. View Data\n");
printf("4. Exit\n");
printf("Choose >> ");
scanf("%d", &choose);
getchar();
switch(choose){
case 1:
inputNilai();
pushMid(value);
printf("Insert Mid Data Success!\n");
break;
case 2:
inputNilai();
popMid(value);
break;
case 3:
cetak();
break;
case 4:
printf("Anda keluar aplikasi");
break;
}
printf("\nPress ENTER to continue...");
getchar();
}
while(choose != 4);
}
PUSH AND POP MID (DIRECT SORTED DLL) CODE IMPLEMENTATION
#include <stdio.h>#include <stdlib.h>
struct node{
int value;
struct node *next, *prev;
} *head = NULL, *tail = NULL, *curr;
void push_mid(int x){
curr = (struct node*)malloc(sizeof(struct node));
curr->value = x;
curr->next = curr->prev = NULL;
if(head == NULL){
head = tail = curr;
}
else if (x < head->value){
//push head
curr->next = head;
head->prev = curr;
head = curr;
}
else if (x > tail->value){
//push tail
tail->next = curr;
curr->prev = tail;
tail = curr;
}
else{
node* temp = head;
while(temp->next->value < x){
temp = temp->next;
}
curr->next = temp->next;
temp->next->prev = curr;
temp->next = curr;
curr->prev = temp;
}
}
void pop(int x){
if (head == NULL){
puts("Pop(x) failed! No Data in LL");
}
else if(head == tail){
//only 1 data
free(head);
head = tail = NULL;
}
else if(x == head->value){
//data located at head
curr = head;
head = head->next;
free(curr);
head->prev = NULL;
}
else if(x == tail->value){
//data located at tail
curr = tail;
tail = tail->prev;
free(curr);
tail->next = NULL;
}
else{
curr = head;
while(curr != NULL && curr->value != x){
curr = curr->next;
}
if(curr == NULL){
puts("Pop(x) failed. x is not found!");
}
else{
curr->next->prev = curr->prev;
curr->prev->next = curr->next;
free(curr);
}
}
}
void print_all(){
curr = head; //point to first data
while( curr != NULL )
{
printf("%d ",curr->value);
curr = curr->next;
}
}
int main()
{
push_mid(15);
push_mid(50);
push_mid(99);
push_mid(20);
push_mid(30);
push_mid(25);
push_mid(100);
pop(200);
pop(50);
pop(15);
pop(100);
pop(30);
push_mid(200);
print_all();
return 0;
}
STACK AND QUEUE
Stack and queue merupakan konsep keluar masuk data.1. Stack
Konsep stack mirip seperti LIFO (Last In First Out). Jadi, data paling akhir yang masuk, data itu yang akan dikeluarkan terlebih dahulu. Pemisalan konsep seperti penumpukkan buku, dimana buku paling atas yaitu buku yang paling terakhir dimasukkan yang akan dikeluarkan terlebih dahulu.
Implementasi Stack: Konversi Infix ke Prefix atau Postfix.
2. Queue
Konsep queue mirip seperti FIFO (First In First Out). Jadi, data yang paling awal masuk, data itulah yang akan dikeluarkan terlebih dahulu. Pemahaman konsep termudah adalah seperti kegiatan mengantri, dimana orang paling depan akan keluar terlebih dahulu.
Jenis Linked List yang digunakan: pushDepan dan popBelakang, pushBelakang dan popDepan.
HASHING DAN HASH TABLES
Pengertian Hashing
Jadi, hashing merupakan teknik yang digunakan untuk mengubah string dengan panjang yang asli menjadi lebih pendek.
Teknik hashing ini biasa digunakan untuk mengambil suatu item dari database. Teknik ini dipilih karena item bisa ditemukan lebih cepat dengan menggunakan kunci hash daripada menggunakan nilai asli.
Hashing juga merupakan konsep mendistribusikan kunci dalam array (table hash) menggunakan fungsi hash.
Fungsi Hash
Sumber: https://en.wikipedia.org/wiki/Hash_function
Pengertian Hash Table
Hash table menjadi tempat penyimpanan string sementara.
Index tabel adalah kunci hashnya, kemudian value tabel adalah string aslinya.
Ukuran hash table bisa lebih sedikit dibandingkan jumlah string asli yang ada, karena beberapa string dapat memiliki kunci hash yang sama.
Contoh Konsep Hash
Soal:
Menyimpan 5 string: define, atan, char, float, exp dengan fungsi hash "ubah karakter dari tiap string menjadi angka mulai dari 0...25"
Dari soal tersebut, maka dapat diklasifikasikan:
a) Index tabel adalah angka 0...25
b) Fungsi hash adalah "ubah karakter dari tiap string menjadi angka mulai dari 0...25"
c) Value tabel adalah define, atan, char, float, exp
Maka, dari penjabaran di atas, dapat disesuaikan bahwa
indeks 0 diisi dengan string atan karena awal karakternya 'a'.
indeks 1 kosong karena tidak ada string yang awal karakternya 'b'.
indeks 2 diisi dengan string char karena awal karakternya 'c'.
indeks 3 diisi dengan string define karena awal karakternya 'd'.
indeks 4 diisi dengan string exp karena awal karakternya 'e'.
indeks 5 diisi dengan string float karena awal karakternya 'f'.
dst
Dari, pengelompokkan di atas, maka didapat hash table sebagai berikut:
Hash Table
Sumber: PPT Binus Maya
Metode-Metode Fungsi Hash
Ada beberapa metode yang digunakan sebagai fungsi hash, diantaranya:
- Mid-square
Metode ini dilakukan dengan:
1) Memangkatkan value (jika value string, convert jadi angka) dengan pangkat dua
2) Mengambil angka di tengah dari hasil pangkat dua tersebut yang kemudian dikonversi menjadi nilai bit
Contoh:
Valuenya adalah 3121. Maka 3121 akan dipangkatkan dengan dua menjadi 9740641. Dari hasil pangkat dua, diambil angka di tengahnya yaitu 406.
Hasil pangkat dua dari 3121 dalam bentuk bit adalah 1001010-0101000010-1100001. Nilai 0101000010 (angka tengah dari hasil pangkat dua 3121) akan diambil menjadi key hashnya.
- Division
Metode ini menggunakan modulus.
Rumusnya bisa dengan menggunakan angka 64 ditambah nilai urutan huruf (1...26)
Jumlah angka yang didapat akan dimodulus dengan 97.
Contohnya:
"COBB" akan disimpan di index = ((64+3) + (64+15) + (64+2) + (64+2)) % 97 = 88
Maka value "COBB" akan disimpan di index h[88].
- Folding
Metode ini menggunakan konsep 'melipat' yaitu dengan memecah value menjadi beberapa bagian yang masing-masing memiliki 2 digit yang kemudian akan dijumlahkan kemudian 2 angka terakhir dari hasil penjumlahan digunakan sebagai indeks hash.
Contoh:
a) 34567
dipecah per 2 digit menjadi: 34, 56, dan 7
kemudian dijumlahkan: 34 + 56 + 7 = 97
maka indeks hash untuk menyimpan value 34567 adalah h[97].
b) 5678
dipecah per 2 digit: 56 dan 78
dijumlahkan: 56 + 78 = 134
diambil 2 angka terakhir: 34
maka indeks hash untuk menyimpan value 5678 adalah h[34].
- Digit Extraction
Metode ini mengambil value dari digit angka tertentu untuk dijadikan kunci hash.
Contoh:
Nilai 14568
akan diambil value dari digit yang ganjil: digit ke-1,3,5 -> 158
maka indeks hash untuk menyimpan value 14568 adalah h[138].
- Rotating Hash
Metode ini merupakan metode tambahan setelah melakukan metode yang lain (folding, mid-square, division, dsb).
Setelah mendapatkan kunci hash dari fungsi hash sebelumnya, maka akan dilakukan rotasi.
Contoh:
Alamat hash sebelumnya -> Alamat hash setelah dirotasi
600101 -> 160010
600102 -> 260010
600103 -> 360010
(Note: value digit paling terakhir, pindah posisi ke paling depan)
Collision
Collision adalah kondisi dimana ada 2 value yang memiliki kunci hash/indeks hash yang sama.
Contoh lanjutan dari 5 string sebelumnya (ada tambahan):
define, atan, char, float, exp, ceil, acos, floor
Pembahasan:
Jika menggunakan fungsi hash "ubah karakter dari tiap string menjadi angka mulai dari 0...25", maka ada beberapa value yang memiliki kunci hash yang sama.
(atan dan acos berada di h[0], char dan ceil berada di h[2], float dan floor berada di h[5]).
Peristiwa ini disebut Collision.
Ada beberapa cara mengatasi Collision:
- Linear Probing
Metode ini akan mencari slot kosong selanjutnya kemudian meletakkan string tersebut di situ.
Contoh soal sebelumnya:
#Jika disesuaikan dengan soal sekarang (sebelum dilakukan Linear Probing) maka:
h[0] = atan, acos
h[1] = null
h[2] = char, ceil
h[3] = define
h[4] = exp
h[5] = float, floor
Setelah ditambahkan beberapa value string di soal baru (acos, ceil, dan floor) maka ada beberapa value yang berada di indeks yang sama.
Dengan menggunakan 'Linear Probing', maka value selanjutnya yang berada di indeks yang sama akan diletakkan pada slot selanjutnya yang kosong, sehingga menjadi:
Kelemahan: Sulit dilakukan pencarian bila terdapat banyak Collision, karena jika ingin mencari ceil mulai dari indeks ke-2 akan lanjut iterasi hingga menemukan value ceil (2->3->4->5->6) sebanyak 5 step.
Implementasi Code:
char data[TABLE_SIZE][100];void linearProbing(int key, char name[]){
if(strcmp(data[key],"") == 0 ){
strcpy(data[key],name);
}else{
for(i=key+1; i<TABLE_SIZE ; i++ ){
if(i == key){
printf("Failed to insert %s because TABLE is FULL\n",name);
break;
}
if(strcmp(data[i],"") == 0 ){
strcpy(data[i],name);
break;
}
if (i == TABLE_SIZE -1) i = -1;
}
}
}
void print(){
for(i = 0;i<TABLE_SIZE;i++){
printf("%d. %s\n",i,data[i]);
}
}
- Chaining
Meletakkan string di slot sebagai sebuah chained list (linked list).
Dalam metode chaining ini, value tetap akan diletakkan pada indeks yang sama, hanya saja dijadikan dalam bentuk linked list. Maka, jika terdapat Collision, kita hanya perlu melakukan iterasi di indeks tersebut saja.
Implementasi Code:
struct list{
char name[100];
struct list* next;
}*head[TABLE_SIZE],*tail[TABLE_SIZE], *curr;
int i;
void chaining(int key, char name[]){
curr = (struct data*) malloc (sizeof(struct list));
strcpy(curr->name,name);
curr->next = 0;
if (head[key] == NULL){
head[key] = tail[key] = curr;
}
else{
tail[key]->next = curr;
tail[key] = curr;
}
}
void view(){
for(i=0 ; i< TABLE_SIZE; i++){
if(head[i] == NULL){
printf("%d. \n");
}
else{
printf("%d. ",i);
curr = head[i];
while (curr != NULL){
printf("%s->", curr->name);
curr = curr->next;
}
puts("");
}
}
}
TREE DAN BINARY TREE
Pengertian Tree
Tree merupakan struktur data yang tidak linear, sifatnya hierarki (bertingkat), dan mewakili hubungan hierarkis di antara objek data.
Tree adalah kumpulan dari satu atau lebih nodes.
Node di pohon dapat disimpan di mana saja dan dihubungkan oleh pointer.
Konsep Binary Tree
Binary Tree merupakan tree yang memiliki anak cabang maksimal 2 pada tiap nodenya.
Tipe Binary Tree:
- Perfect Binary Tree
Binary Tree yang tiap nodenya ( kecuali leaf) memiliki dua child dan tiap subtree harus mempunyai panjang path yang sama.
- Complete Binary Tree
Mirip dengan Full Binary Tree, namun tiap subtree boleh memiliki panjang path yang berbeda. Node kecuali leaf memiliki 0 atau 2 child.
- Skewed Binary Tree
Binary Tree yang semua nodenya (kecuali leaf) hanya memiliki satu child.
- Balanced Binary Tree
Merupakan pohon biner di mana tidak ada daun yang lebih jauh dari akar daripada daun lainnya (skema penyeimbangan yang berbeda memungkinkan definisi yang berbeda dari "jauh lebih jauh").
Property Binary Tree
Formula untuk menghitung jumlah node per level: 2^n
Level dimulai dari n = 0.
Maka, jumlah maksimum nodes dari tree dengan height 3 adalah 1+2+4+8 = 15.
Minimum tinggi binary tree dari n nodes adalah 2log(n).
Maksimum tinggi binary tree dari n nodes adalah n - 1. => (skewed binary tree memiliki height tree maksimum).
Implementasi Binary Tree
- Menggunakan Array
Indeks di array mewakili nomor node
Indeks untuk node root adalah 0.
Indeks Anak Kiri adalah 2p + 1 (p adalah indeks parent)
Indeks Anak Kanan adalah 2p+2
Indeks parent adalah (p-1)/2
- Menggunakan Linked List
struct node {
int data;
struct node *left;
struct node *right;
struct node *parent;
};
struct node *root = NULL;
IMPLEMENTASI HASHING DALAM BLOCKCHAIN
Berdasarkan pembahasan di atas, maka hashing ini kerap kali digunakan dalam konsep blockchain. Dikenal dengan metode 'Kriptografi' yaitu ilmu yang mempelajari teknik-teknik matematika yang berhubungan dengan aspek keamanan informasi, seperti kerahasiaan data, keabsahan data, integritas data, serta autentikasi data.
Pada prinsipnya, Kriptografi memiliki 4 komponen utama yaitu :
1. Plaintext, yaitu pesan yang dapat dibaca
2. Ciphertext, yaitu pesan acak yang tidak dapat dibaca
3. Key, yaitu kunci untuk melakukan teknik kriptografi
4. Algorithm, yaitu metode untuk melakukan enkrispi dan dekripsi
Kemudian, proses dasar yang umumnya ada pada Kriptografi yaitu:
1. Enkripsi (Encryption), proses menjadikan pesan yang dapat dibaca (plaintext) menjadi pesan acak yang tidak dapat dibaca (ciphertext).
2. Dekripsi (Decryption), proses kebalikan dari enkripsi dimana proses ini akan mengubah ciphertext menjadi plaintext dengan menggunakan algoritma "pembalik" dan key yang sama.
Pada prinsipnya, Kriptografi memiliki 4 komponen utama yaitu :
1. Plaintext, yaitu pesan yang dapat dibaca
2. Ciphertext, yaitu pesan acak yang tidak dapat dibaca
3. Key, yaitu kunci untuk melakukan teknik kriptografi
4. Algorithm, yaitu metode untuk melakukan enkrispi dan dekripsi
Kemudian, proses dasar yang umumnya ada pada Kriptografi yaitu:
1. Enkripsi (Encryption), proses menjadikan pesan yang dapat dibaca (plaintext) menjadi pesan acak yang tidak dapat dibaca (ciphertext).
2. Dekripsi (Decryption), proses kebalikan dari enkripsi dimana proses ini akan mengubah ciphertext menjadi plaintext dengan menggunakan algoritma "pembalik" dan key yang sama.
Kode-kode asing yang sering kita lihat dalam proses encryption dan decryption merupakan salah satu contoh hash. Hash mampu mengubah setiap data yang mengalami perubahan dengan nilai unik sendiri.
Nilai berharga sebuah data saat ini berpotensi dibobol atau diketahui oleh orang lain. Salah satu teknik mengakalinya ialah dengan pemberian kode unik.
Ada sejumlah hash yang digunakan saat ini seperti:
- SHA256
Hash ini digunakan pada Bitcoin khusus proses transaksi dan perhitungan nilai Hash.
- RIPEMD160
Hash RIPEMD160 merupakan singkat dari Race Integrity Primitive Evaluation Message Digest. Konsep dari algoritma dari hash ini dikembangkan oleh MD4. Jumlah data transaksi yang dihasilkan lebih kecil dibandingkan SHA256 yaitu hanya 160 bit.
- Monero
Pada Monero, penerapan pada keamanan data menggunakan sejumlah Hash, mulai dari Keccak, Blake, Grostl, JH, dan Skein pada CryptoNote. Konsep dari Monero yang sangat kompleks seakan membuatnya dijuluki sebagai fully anonymous.
Jadi, konsep Hash ini sangat penting dan sering digunakan dalam konsep Blockchain. Teknik Hash ini digunakan untuk melakukan enkripsi terhadap data dengan mengubah value asli dari data menjadi sebuah kode yang unik yang bertujuan untuk menjaga privasi data user dan terhindar dari pencurian data. Konsep ini sering kita dengar seperti dalam penggunaannya di Bitcoin.
INFIX TO PREFIX OR POSTFIX USING STACK AND EXPRESSION TREE
CONVERSION USING STACK
Syaratnya semua operator masuk stack dan semua operand masuk ke string.
Conversion Infix to Postfix:
- dibaca dari kiri ke kanan
- Bisa cek manual dengan menghitung 2 operand dan 1 operator dari kiri hingga selesai
- Syarat: Jika operator lama tingkatnya lebih tinggi atau setara dari operator yang baru masuk, maka masukkan operand sebelumnya ke string. Lalu, jika ada tanda '(' maka masukkan semua operator yang ada dan dikeluarkan secara stack ketika ketemu tanda ')'.
String
|
Stack
|
Postfix String
|
Operation
|
(A-B/C)*(D/E+F)
| |||
(A-B/C)*(D/E+F)
|
(
|
push(()
| |
(A-B/C)*(D/E+F)
|
(
|
A
|
add(A)
|
(A-B/C)*(D/E+F)
|
( -
|
A
|
push(-)
|
(A-B/C)*(D/E+F)
|
( -
|
AB
|
add(B)
|
(A-B/C)*(D/E+F)
|
( - /
|
AB
|
push(/)
|
(A-B/C)*(D/E+F)
|
( - /
|
ABC
|
add(C)
|
(A-B/C)*(D/E+F)
|
ABC/-
|
pop(/), pop(-), pop(()
| |
(A-B/C)*(D/E+F)
|
*
|
ABC/-
|
push(*)
|
(A-B/C)*(D/E+F)
|
* (
|
ABC/-
|
push(()
|
(A-B/C)*(D/E+F)
|
* (
|
ABC/-D
|
add(D)
|
(A-B/C)*(D/E+F)
|
* ( /
|
ABC/-D
|
push(/)
|
(A-B/C)*(D/E+F)
|
* ( /
|
ABC/-DE
|
add(E)
|
(A-B/C)*(D/E+F)
|
* ( +
|
ABC/-DE/
|
pop(/), push(+)
|
(A-B/C)*(D/E+F)
|
* ( +
|
ABC/-DE/F
|
add(F)
|
(A-B/C)*(D/E+F)
|
ABC/-DE/F+*
|
pop(+), pop((), pop(*)
|
Conversion Infix to Prefix:
- dibaca dari kanan ke kiri
- Bisa cek manual dengan menghitung 2 operand dan 1 operator dari kanan hingga selesai
- Syarat: Jika operator lama tingkatnya lebih tinggi dari operator yang baru masuk, maka masukkan operand sebelumnya ke string. Lalu, jika ada tanda ')' maka masukkan semua operator yang ada dan dikeluarkan secara stack ketika ketemu tanda '('.
String
|
Stack
|
Prefix String
|
Operation
|
(A-B/C)*(D/E+F)
| |||
(A-B/C)*(D/E+F)
|
)
|
push())
| |
(A-B/C)*(D/E+F)
|
)
|
F
|
add(F)
|
(A-B/C)*(D/E+F)
|
) +
|
F
|
push(+)
|
(A-B/C)*(D/E+F)
|
) +
|
EF
|
add(E)
|
(A-B/C)*(D/E+F)
|
) + /
|
EF
|
push(/)
|
(A-B/C)*(D/E+F)
|
) + /
|
DEF
|
add(D)
|
(A-B/C)*(D/E+F)
|
+/DEF
|
pop(/), pop(+), pop())
| |
(A-B/C)*(D/E+F)
|
*
|
+/DEF
|
push(*)
|
(A-B/C)*(D/E+F)
|
) *
|
+/DEF
|
push())
|
(A-B/C)*(D/E+F)
|
) *
|
C+/DEF
|
add(C)
|
(A-B/C)*(D/E+F)
|
) * /
|
C+/DEF
|
push(/)
|
(A-B/C)*(D/E+F)
|
) * /
|
BC+/DEF
|
add(B)
|
(A-B/C)*(D/E+F)
|
) * -
|
/BC+/DEF
|
pop(/), push(-)
|
(A-B/C)*(D/E+F)
|
) * -
|
A/BC+/DEF
|
add(A)
|
(A-B/C)*(D/E+F)
|
*-A/BC+/DEF
|
pop(-), pop(*), pop())
|
CONVERSION USING EXPRESSION TREE
Alur baca konsep prefix : Parent - Left - Right
Alur baca konsep postfix: Left - Right - Parent
Alur baca konsep infix : Left - Parent - Right
INFIX
POSTFIX
PREFIX
BINARY SEARCH TREE
Binary Search Tree atau biasa disingkat BST merupakan salah satu struktur data yang mempercepat pencarian dan pengurutan (sorting), dengan metode insertion dan deletion yang mudah. BST dikenal juga sebagai binary tree yang diurutkan (sorted version of Binary Tree).
B. Properti Binary Tree
Berikut ini penjelasan properti di Binary Search Tree:
Sumber: Geeksforgeeks.org
Menggunakan contoh dari gambar di atas, maka akan dijelaskan macam-macam istilah dalam BST:
- Root : Berperan sebagai akar paling atas/pusatnya tree, yaitu angka 8.
- Parent : Node yang berada satu level di atas suatu node tertentu, contohnya angka 3 adalah parent node dari angka 1 dan angka 6.
- Child : Node yang berada satu level di bawah suatu node tertentu, contohnya angka 14 adalah child node dari angka 10.
- Leaf : Node yang tidak memiliki child, contohnya angka 1, 4, 7, dan 13.
- Sibling : Node yang memiliki parent yang sama, contohnya angka 1 dan angka 6.
C. Konsep Binary Search Tree
Binary Tree memiliki akar atau yang disebut root node dan memiliki 2 sisi cabang tree yaitu tree cabang kiri dan tree cabang kanan.
Tree cabang kiri akan selalu menampung value yang lebih kecil dari value parentnya, sedangkan
tree cabang kanan akan selalu menampung value yang lebih besar dari value parentnya.
Binary Tree memiliki syarat yaitu batas maksimum anak dari node parent adalah 2 child nodes.
- Cek apakah nilai 4 lebih kecil/besar dari root 8, ternyata lebih kecil maka masuk ke cabang tree kiri.
- Cek apakah cabang di root 8 sudah ada 2 child nodes? Ya, maka perlu turun cabang.
- Cek apakah 4 lebih kecil/besar dari 3, ternyata lebih besar maka masuk ke cabang tree kanan.
- Cek apakah cabang di node 3 sudah ada 2 child nodes? Ya, maka perlu turun cabang.
- Cek apakah 4 lebih kecil/besar dari 6, ternyata lebih kecil maka masuk ke cabang tree kiri.
- Cek apakah cabang di node 6 sudah ada 2 child nodes? Tidak/belum, maka value 4 diletakkan di cabang sebelah kiri dari parent node 6.
D. Operasi Binary Search Tree
//Buat struct untuk node
struct node{
int key;
struct node *left;
struct node *right;
};
//Pembuatan node baru
struct node *newNode(int x){
//Pesan space memory ke komputer
struct node *currNewNode = (struct node*) malloc(sizeof(struct node));
//Masukkan value
currNewNode->key = x;
//Set child kiri NULL
currNewNode->left = NULL;
//Set child kanan NULL
currNewNode->right = NULL;
//Return alamat dari currNewNode;
return currNewNode;
}
//Insert new node
struct node *add(struct node *root, int x){
//Saat ketemu root yang kosong, new node diletakkan di sini
if(root == NULL) return newNode(x);
//Jika value lebih kecil dari root, rekursif ke child kiri
else if(x < root->key) root->left = add(root->left, x);
//Jika value lebih besar dari root, rekursif ke child kanan
else if(x > root->key) root->right = add(root->right, x);
//Return alamat root
return root;
}
//Print BST secara Infix
void printAllInfix(struct node *root){
//Kalau ketemu rootnya NULL, maka balik
if(root == NULL) return;
//Rekursif ke child kiri
printAllInfix(root->left);
//Print value
printf(" %d ", root->key);
//Rekursif ke child kanan
printAllInfix(root->right);
}
//Print BST secara Prefix
void printAllPrefix(struct node *root){
//Kalau ketemu rootnya NULL, maka balik
if(root == NULL) return;
//Print value
printf(" %d ", root->key);
//Rekursif ke child kiri
printAllPrefix(root->left);
//Rekursif ke child kanan
printAllPrefix(root->right);
}
//Print BST secara Postfix
void printAllPostfix(struct node *root){
//Kalau ketemu rootnya NULL, maka balik
if(root == NULL) return;
//Rekursif ke child kiri
printAllPostfix(root->left);
//Rekursif ke child kanan
printAllPostfix(root->right);
//Print value
printf(" %d ", root->key);
}
//Hapus tree
struct node *freeAll(struct node *root){
if(root == NULL) return NULL;
root->left = freeAll(root->left);
root->right = freeAll(root->right);
free(root);
return NULL;
}
//Metode deletion dena=gan menggunakan value terbesar di subtree kiri
struct node *predecessor(struct node *root){
//Turun ke cabang kiri
struct node *curr = root->left;
//Selama belum turunannya belum paling kanan (paling besar di cabang kirinya root), turun lagi
while(curr->right != NULL){
curr = curr->right;
}
//Jika sudah paling kanan di cabang kirinya root, maka return nilainya
return curr;
}
struct node *deleteValue(struct node *root, int x){
//Jika data tidak ada di dalam tree
if(root == NULL) return NULL;
else if(x < root->key) root->left = deleteValue(root->left, x);
else if(x > root->key) root->right = deleteValue(root->right, x);
//Jika data ditemukan
else{
//Jika node tidak memiliki child, atau memiliki 1 child
if(root->left == NULL || root->right == NULL){
struct node *temp = NULL;
if(root->left != NULL) temp = root->left;
else temp = root->right;
//Jika tidak memiliki child
if(temp == NULL){
temp = root;
root = NULL;
}
//Jika memiliki 1 child
else{
*root = *temp;
}
free(temp);
}
//Node punya 2 child
else{
//Menggunakan predecessor: Menggunakan value node paling besar di
//cabang tree kiri untuk dijadikan parent
struct node *temp = predecessor(root);
root->key = temp->key;
//Delete
root->left = deleteValue(root->left, temp->key);
}
}
return root;
}
//Buat struct untuk node
struct node{
int key;
struct node *left;
struct node *right;
};
//Pembuatan node baru
struct node *newNode(int x){
//Pesan space memory ke komputer
struct node *currNewNode = (struct node*) malloc(sizeof(struct node));
//Masukkan value
currNewNode->key = x;
//Set child kiri NULL
currNewNode->left = NULL;
//Set child kanan NULL
currNewNode->right = NULL;
//Return alamat dari currNewNode;
return currNewNode;
}
//Insert new node
struct node *add(struct node *root, int x){
//Saat ketemu root yang kosong, new node diletakkan di sini
if(root == NULL) return newNode(x);
//Jika value lebih kecil dari root, rekursif ke child kiri
else if(x < root->key) root->left = add(root->left, x);
//Jika value lebih besar dari root, rekursif ke child kanan
else if(x > root->key) root->right = add(root->right, x);
//Return alamat root
return root;
}
//Print BST secara Infix
void printAllInfix(struct node *root){
//Kalau ketemu rootnya NULL, maka balik
if(root == NULL) return;
//Rekursif ke child kiri
printAllInfix(root->left);
//Print value
printf(" %d ", root->key);
//Rekursif ke child kanan
printAllInfix(root->right);
}
//Print BST secara Prefix
void printAllPrefix(struct node *root){
//Kalau ketemu rootnya NULL, maka balik
if(root == NULL) return;
//Print value
printf(" %d ", root->key);
//Rekursif ke child kiri
printAllPrefix(root->left);
//Rekursif ke child kanan
printAllPrefix(root->right);
}
//Print BST secara Postfix
void printAllPostfix(struct node *root){
//Kalau ketemu rootnya NULL, maka balik
if(root == NULL) return;
//Rekursif ke child kiri
printAllPostfix(root->left);
//Rekursif ke child kanan
printAllPostfix(root->right);
//Print value
printf(" %d ", root->key);
}
//Hapus tree
struct node *freeAll(struct node *root){
if(root == NULL) return NULL;
root->left = freeAll(root->left);
root->right = freeAll(root->right);
free(root);
return NULL;
}
//Metode deletion dena=gan menggunakan value terbesar di subtree kiri
struct node *predecessor(struct node *root){
//Turun ke cabang kiri
struct node *curr = root->left;
//Selama belum turunannya belum paling kanan (paling besar di cabang kirinya root), turun lagi
while(curr->right != NULL){
curr = curr->right;
}
//Jika sudah paling kanan di cabang kirinya root, maka return nilainya
return curr;
}
struct node *deleteValue(struct node *root, int x){
//Jika data tidak ada di dalam tree
if(root == NULL) return NULL;
else if(x < root->key) root->left = deleteValue(root->left, x);
else if(x > root->key) root->right = deleteValue(root->right, x);
//Jika data ditemukan
else{
//Jika node tidak memiliki child, atau memiliki 1 child
if(root->left == NULL || root->right == NULL){
struct node *temp = NULL;
if(root->left != NULL) temp = root->left;
else temp = root->right;
//Jika tidak memiliki child
if(temp == NULL){
temp = root;
root = NULL;
}
//Jika memiliki 1 child
else{
*root = *temp;
}
free(temp);
}
//Node punya 2 child
else{
//Menggunakan predecessor: Menggunakan value node paling besar di
//cabang tree kiri untuk dijadikan parent
struct node *temp = predecessor(root);
root->key = temp->key;
//Delete
root->left = deleteValue(root->left, temp->key);
}
}
return root;
}
TUGAS CODE REVIEW UTS
Pada tugas ini, saya menambahkan validasi nama dan qty, lalu nama yang baru di-add tidak boleh sama dengan data yang sudah ada. Jika sudah ada maka langsung ke function edit. Lalu ada fitu viewProductList() untuk melihat daftar belanjaan sementara di keranjang. Lalu, ada fitur checkout dimana akan diprint bill hasil pembelian dan program akan exit.
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
char name[51];
int qty;
long long int price;
struct product{
char name[51];
int qty;
long long int price;
struct product *prev;
struct product *next;
} *head = NULL, *tail = NULL, *current;
void printMenu(){
printf("===== WELCOME TO ANGELIA'S DREAMMERS MARKET =====\n");
printf("1. Add New Product\n");
printf("2. Edit Product's Quantity\n");
printf("3. Delete Product\n");
printf("4. View Product List\n");
printf("5. Checkout\n");
printf(">> Choose: ");
}
void inputName(){
do{
printf("Insert Product's Name [1-50]\t: ");
scanf("%[^\n]", name);
getchar();
}
while(strlen(name) < 1 || strlen(name) > 50);
}
void inputQty(){
do{
printf("Insert Product's Qty [1..100]\t: ");
scanf("%d", &qty);
getchar();
}
while(qty < 1 || qty>100);
}
long long int randomPrice(){
long lower = 100;
long upper = 999000;
return (rand() % (upper-lower+1) + lower);
}
//Sorted push secara ascending bdk nama produk
void push(char name[51], int qty, double price){
//Pesan memori dan Set data
current = (struct product*) malloc(sizeof(struct product));
strcpy(current->name, name);
current->qty = qty;
current->price = price;
current->prev = NULL;
current->next = NULL;
//Kalau data pertama
if(head == NULL){
head = tail = current;
}
//Kalau data abjad paling depan, push depan
else if(strcmp(current->name, head->name) < 0){
head->prev = current;
current->next = head;
head = current;
}
//Kalau data abjad paling belakang, push belakang
else if(strcmp(current->name, tail->name) > 0){
tail->next = current;
current->prev = tail;
tail = current;
}
//Jika posisi di antara, push mid
else{
struct product *temp = head;
while(strcmp(current->name, temp->next->name) > 0){
temp = temp->next;
}
current->next = temp->next;
temp->next = current;
current->prev = temp;
temp->next->prev = current;
}
}
void pop(char name[51]){
//Jika hanya 1 data
if(strcmp(name, head->name) == 0 && head == tail){
printf("\nProduct %s deleted successfully!\n", current->name);
free(head);
head = tail = NULL;
}
//Data ditemukan di awal
else if(strcmp(name, head->name) == 0){
current = head;
head = head->next;
printf("\nProduct %s deleted successfully!\n", current->name);
free(current);
head->prev = NULL;
}
//Data ditemukan di akhir
else if(strcmp(name, tail->name) == 0){
current = tail;
tail = tail->prev;
printf("\nProduct %s deleted successfully!\n", current->name);
free(current);
tail->next = NULL;
}
//Data ditemukan di tengah
else{
current = head;
while(current != NULL){
if(strcmp(name, current->name) == 0) break;
current = current->next;
}
//Data tidak ada
if(current == NULL) printf("Product name is not found!\n");
//Data ada
else{
current->next->prev = current->prev;
current->prev->next = current->next;
printf("\nProduct %s deleted successfully!\n", current->name);
free(current);
}
}
}
void editProduct(char name[51]){
//Cek ada nama produk yang sama, jika ada maka pindah ke bagian edit qty langsung
current = head;
while(current != NULL){
if(strcmp(name, current->name) == 0) break;
current = current->next;
}
//Jika nama product belum ada
if (current == NULL) printf("Product name is not found!\n");
else{
printf("===== EDIT QTY PRODUCT =====\n");
inputQty();
current->qty = qty;
printf("\nPRODUCT %s QTY HAS BEEN CHANGED SUCCESSFULLY!\n", current->name);
}
}
void addProduct(){
printf("===== ADD NEW PRODUCT =====\n");
inputName();
//Cek ada nama produk yang sama, jika ada maka pindah ke bagian edit qty langsung
current = head;
while(current != NULL){
if(strcmp(name, current->name) == 0) break;
current = current->next;
}
//Jika nama product belum ada
if(current == NULL){
inputQty();
//Set random price (per item), untuk total price akan dihitung saat checkout
price = randomPrice();
push(name, qty, price);
printf("\nINSERT NEW PRODUCT SUCCESS!\n");
}
//Jika nama product sudah ada, langsung edit
else{
printf("\nProduct's name is already exist!\n");
editProduct(name);
}
}
void deleteProduct(){
printf("===== DELETE PRODUCT =====\n");
inputName();
pop(name);
}
void viewProductList(int choose){
long long int total = 0;
int index = 0;
if(choose == 4) printf("============================== CURRENT TROLLEY LIST ==============================\n");
else if(choose == 5) printf("============================ DREAMMERS MARKET RECEIPT ============================\n");
printf("|| %3s. || %-20s || %3s || %18s || %15s ||\n", "No", "Product Name", "Qty", "Price (per item)", "Total Price");
current = head;
while(current != NULL){
printf("|| %3d. || %-20s || %3d || %-8s %9ld || %-5s %9ld ||\n", index+1, current->name, current->qty, "Rp.", current->price, "Rp.", current->qty * current->price);
total += current->qty * current->price;
current = current->next;
index++;
}
if(choose == 4){
printf("==================================================================================\n");
puts("");
printf("GRAND TOTAL\t: Rp. %ld\n", total);
}
else if(choose == 5){
printf("==================================================================================\n");
puts("");
printf("TOTAL PAYMENT : Rp. %ld\n", total);
printf("Kindness is free\n\n");
}
}
void byeGreeting(){
printf("Thank you for coming to Angelia's Dreammers Market\n");
printf("Created By: Angelia \(2301854492\)");
}
int main(){
int choose = -1;
do{
system("cls");
printMenu();
scanf("%d", &choose);
getchar();
switch(choose){
case 1:
addProduct();
break;
case 2:
if(head == NULL) printf("No Data!\n");
else{
inputName();
editProduct(name);
}
break;
case 3:
if(head == NULL) printf("No Data!\n");
else deleteProduct();
break;
case 4:
//View Temporary Trolley List
if(head == NULL) printf("No Data!\n");
else viewProductList(choose);
break;
case 5:
//Checkout
if(head == NULL) printf("You have bought nothing!\n");
else viewProductList(choose);
byeGreeting();
break;
}
if(choose<5 && choose>0){
printf("\nPress any key to continue...");
getchar();
}
}
while(choose != 5);
return 0;
}
Berikut ini link google drive untuk file .cpp dan .exe dan summary dari tugas ini:
UAS
AVL TREE
Setelah mengikuti perkuliahan online melalui video conference, telah dibahas materi mengenai AVL Tree. Berikut ini pembahasan rangkuman mengenai materi AVL Tree.
Konsep dasarnya berawal dari kelemahan Binary Search Tree. Jika kita selalu menginsert data yang lebih besar, maka tree menjadi tidak seimbang karena anak cabang kanan akan lebih panjang daripada kiri. Hal ini akan membuat waktu pencarian data menjadi lebih lama. Untuk itu, dengan menggunakan AVL Tree sebagai salah satu solusi tree untuk mengatasi ketidakseimbangan anak cabang dapat teratasi sehingga waktu pencarian data akan lebih efisien.
AVL Tree merupakan self-balancing BST pertama yang ditemukan. Tree ini ditemukan oleh G.M. Adelson - Veleskii dan E.M. Landis.
Konsep AVL Tree
Cabang dinyatakan balance apabila jumlah anak kiri/kanan - jumlah anak kanan/kiri hasilnya tidak lebih dari 1. Jika perbedaan jumlah anak cabang kiri dan kanan lebih dari 1, maka tree dinyatakan tidak balance.
Kemudian, proses pengecekan tree balance adalah dengan mengecek dari urutan terbawah lalu naik ke atas. Jika ditemukan parent memiliki anak cabang yang tidak balance maka akan dilakukan rotation untuk mengubah tree agar menjadi balance.
Penerapan AVL Tree
Penerapan Rebalance AVL Tree
Kemudian, dilakukan rotasi kedua yaitu rotasi ke kanan agar anak cabang kiri dan kanan root seimbang. Node value 40 akan rotasi ke kanan menjadi root dan node value 50 akan menjadi anak cabang kanan root. Kemudian, node value 45 dan cabangnya akan menjadi anak cabang kiri dari node value 50. Dengan demikian, tree telah balance, dimana anak cabang kiri root dan anak cabang kanan root sama-sama memiliki tinggi 3 dan bedanya (3-3) adalah 0.
Konsep dasarnya berawal dari kelemahan Binary Search Tree. Jika kita selalu menginsert data yang lebih besar, maka tree menjadi tidak seimbang karena anak cabang kanan akan lebih panjang daripada kiri. Hal ini akan membuat waktu pencarian data menjadi lebih lama. Untuk itu, dengan menggunakan AVL Tree sebagai salah satu solusi tree untuk mengatasi ketidakseimbangan anak cabang dapat teratasi sehingga waktu pencarian data akan lebih efisien.
Hasil BST Tree Hasil AVL Tree
AVL Tree merupakan self-balancing BST pertama yang ditemukan. Tree ini ditemukan oleh G.M. Adelson - Veleskii dan E.M. Landis.
Konsep AVL Tree
Cabang dinyatakan balance apabila jumlah anak kiri/kanan - jumlah anak kanan/kiri hasilnya tidak lebih dari 1. Jika perbedaan jumlah anak cabang kiri dan kanan lebih dari 1, maka tree dinyatakan tidak balance.
Kemudian, proses pengecekan tree balance adalah dengan mengecek dari urutan terbawah lalu naik ke atas. Jika ditemukan parent memiliki anak cabang yang tidak balance maka akan dilakukan rotation untuk mengubah tree agar menjadi balance.
Penerapan AVL Tree
- Insertion
Berikut ini langkah melakukan insertion pada AVL Tree:
1. Melakukan insert dengan konsep seperti BST.
2. Dilakukan pengecekan terhadap jalur dari penginputan node hingga ke root, apakah ada parent tree yang memiliki jumlah anak cabang yang tidak seimbang, maka tree akan dibuat balance dengan melakukan rotation.
- Deletion
Berikut ini langkah melakukan deletion pada AVL Tree:
1. Dilakukan prosedur delete node sesuai konsep BST.
2. Dilakukan pengecekan balance tree pada parent dari node yang di delete hingga ke root. Jika tidak seimbang, maka dilakukan rotation.
Penerapan Rebalance AVL Tree
- Single Rotation
Dilakukan jika anak cabang dari node yang dimasukkan yang tidak balance sejalur dengan root (left-left atau right-right). Kasus yang bisa terjadi:
1. Node tertinggi ada di bagian sub tree kiri dari anak cabang kiri root.
2. Node tertinggi ada di bagian sub tree kanan dari anak cabang kanan root.
Contoh Insertion:
Telah dilakukan insert node dengan value 12 dengan konsep sesuai BST. Kemudian, dilakukan pengecekan terhadap jalur searah hingga ke root, apakah ada tree yang anak cabangnya tidak balance. Ternyata, rootnya memiliki cabang yang tidak balance. Dapat dilihat bahwa anak cabang kiri dari root memiliki tinggi 4 sedangkan anak cabang kanan dari root memiliki tinggi 2. Jika dikurangi (4-2) maka hasilnya adalah 2 dan hal ini telah melanggar ketentuan AVL Tree. Maka dari itu, dilakukan rebalance AVL Tree. Terlihat bahwa garis jalur tidak belok (sub tree kiri pada anak cabang kiri root), maka dilakukan single rotation. Hasilnya menjadi:
Dapat dilihat bahwa telah terjadi single rotation ke kanan karena anak cabang kiri tidak seimbang. Node dengan value 22 berotasi ke kanan menjadi root, kemudian node dengan value 30 akan menjadi anak cabang kanan dari root. Untuk node dengan value 27 akan menjadi anak cabang kiri dari 30.
Contoh Deletion:
Akan dilakukan deletion pada node dengan value 60. Maka, diambil node dari anak cabang kiri dengan value paling besar. Karena di contoh hanya ada 1 node pada anak cabang kiri, maka node dengan value 55 akan menggantikan posisi node value 60.
Setelah posisi node berpindah, maka node value 55 menjadi tidak balance karena memiliki 0 anak cabang kiri dan 2 anak cabang kanan (beda 2). Maka dilakukan rotate ke kiri agar kembali seimbang sehingga node value 65 akan menjadi parentnya dan node value 55 akan menjadi anak cabang kiri dari node value 65.
Dilanjutkan kembali pengecekan jalur ke atas yaitu root 50. Ternyata, anak cabang kiri tingginya 4 dan anak cabang kanan tingginya 2 sehingga beda 2 dan melanggar konsep AVL Tree. Karena node yang menjadi penyebab tree tidak seimbang adalah node value 42 dan letaknya sebagai sub tree kanan pada anak cabang kiri root sehingga akan dilakukan double rotation.
Untuk penjelasan lanjutan double rotation, akan dilanjutkan pada section double rotation di bawah.
- Double Rotation
Dilakukan jika anak cabang dari node yang dimasukkan yang tidak balance memiliki jalur yang bengkok dari root (left-right atau right-left). Kasus yang bisa terjadi:
1. Node tertinggi ada di bagian sub tree kanan dari anak cabang kiri root.
2. Node tertinggi ada di bagian sub tree kiri dari anak cabang kanan root.
Contoh Insertion:
Telah dilakukan insert node dengan value 26 dengan konsep sesuai BST. Kemudian, dilakukan pengecekan terhadap jalur searah hingga ke root, apakah ada tree yang anak cabangnya tidak balance. Ternyata, rootnya memiliki cabang yang tidak balance. Dapat dilihat bahwa anak cabang kiri dari root memiliki tinggi 4 sedangkan anak cabang kanan dari root memiliki tinggi 2. Jika dikurangi (4-2) maka hasilnya adalah 2 dan hal ini telah melanggar ketentuan AVL Tree. Maka dari itu, dilakukan rebalance AVL Tree dengan tujuan mengubah sub tree menjadi searah dengan anak cabang kiri root. Terlihat bahwa garis jalur belok (kiri-kanan), maka dilakukan double rotation karena node tertinggi ada di bagian kanan dari anak cabang kiri dari root.
Hasil rotasi pertama menjadi:
Dilakukan rotate ke kiri sehingga node dengan value 27 menjadi parent dan node dengan value 22 berpindah menjadi anak cabang kiri dari node dengan value 27. Untuk cabang node dengan value 24 akan menjadi anak cabang dari node dengan value 22. Dengan begitu, jalur nodenya sudah berada di bagian kiri dari anak cabang kiri root sehingga dapat dilakukan rotation kedua.
Hasil rotasi kedua menjadi:
Dilakukan rotate ke kanan sehingga node dengan value 27 menjadi root dan node dengan value 30 menjadi anak cabang kanan root. Kemudian untuk node dengan value 29 akan menjadi anak cabang dari node dengan value 30. Dengan begitu, tree akan menjadi balance sesuai dengan aturan AVL Tree. Node value 24 memiliki 0 anak cabang kiri dan 1 anak cabang kanan (OK). Node value 22 memiliki anak cabang kiri dan kanan dengan tinggi 2 (OK). Root value 27 memiliki anak cabang kiri dan kanan dengan tinggi 3 (OK).
Contoh Deletion:
Melanjutkan contoh kasus pada deletion di section single rotation di atas.
Dilanjutkan kembali pengecekan jalur ke atas yaitu root 50. Ternyata, anak cabang kiri tingginya 4 dan anak cabang kanan tingginya 2 sehingga beda 2 dan melanggar konsep AVL Tree. Karena node yang menjadi penyebab tree tidak seimbang adalah node value 42 dan letaknya sebagai sub tree kanan pada anak cabang kiri root sehingga akan dilakukan double rotation.
Pertama, dilakukan rotasi ke kiri supaya sub tree searah dengan anak cabang kiri root. Node value 40 akan menjadi parent dan node value 25 akan menjadi anak cabang kiri dari parent 40. Kemudian anak cabang node value 30 akan menjadi anak cabang kanan dari node value 25.
Kemudian, dilakukan rotasi kedua yaitu rotasi ke kanan agar anak cabang kiri dan kanan root seimbang. Node value 40 akan rotasi ke kanan menjadi root dan node value 50 akan menjadi anak cabang kanan root. Kemudian, node value 45 dan cabangnya akan menjadi anak cabang kiri dari node value 50. Dengan demikian, tree telah balance, dimana anak cabang kiri root dan anak cabang kanan root sama-sama memiliki tinggi 3 dan bedanya (3-3) adalah 0.
B-TREE
Pengertian B-Tree
B-Tree merupakan struktur data yang memfasilitasi pengaksesan data yang lebih cepat dengan membuat dan menggunakan index untuk mengakses data dalam jumlah besar. B-Tree cocok digunakan untuk membuat kamus dengan menyimpan keys dan merekamnya.
Mirip dengan BST yang disebut two-way tree, B-Tree merupakan M-way tree dimana M merupakan jumlah maksimal children yang bisa dimiliki node dan jumlah data dalam tiap node maksimal M-1.
Sifat-Sifat B-Tree
- Setiap node memiliki paling banyak M children.
- Setiap node (kecuali root) memiliki paling sedikit M/2 children.
- Root memiliki minimal 2 children jika ia bukan leaf node.
- Node bukan leaf dengan k children memiliki k-1 keys.
- Semua data diolah dalam urutan sorted.
- Semua leaves node berada di level yang sama (level paling bawah).
B-Tree
B-Tree order 2: Memiliki 1 data dan 2 children.
B-Tree order 3: Memiliki 2 data dan 3 children.
B-Tree order 4: Memiliki 3 data dan 4 children.
B-Tree order 5: Memiliki 4 data dan 5 children.
dan seterusnya.
Semua data disusun berurutan pada saat proses insertion dengan ketentuan data di sub-tree kiri lebih kecil dari node dan data di sub-tree kanan lebih besar dari node.
Operasi B-Tree
1. SEARCHING
Operasi ini digunakan untuk mencari value yang ada di tree. Untuk operasi searching ini mirip dengan BST, tinggal ditambahkan beberapa fitur.
2. INSERTION
a) Memasukkan data baru A.
b) Mencari posisi peletakkan data A dengan sistem seperti BST (lebih kecil ke kiri, lebih besar ke kanan). Posisi new data selalu berada pada salah satu leaf.
c1) Untuk 2-3 Tree:
- Jika leaf 2-node, maka langsung letakkan data A dan selesai
- Jika leaf sudah 3-node, maka push data di tengah ke parent, lalu pecah data kiri dan data kanan menjadi children node terpisah terhadap parent yang baru saja di push.
c2) Untuk m-Tree:
- Jika leaf m-1 node, maka langsung letakkan data A dan selesai
- Jika leaf sudah m node, maka push data di tengah parent, lalu pecah data kiri dan data kanan menjadi children node terpisah terhadap parent yang baru saja di push.
d) Cek parent secara rekursif.
Contoh:
3. DELETION
a) Menentukan target value key yang ingin dihapus.
b) Mengikuti prosedur BST dengan mencari leaf node untuk mereplace targeted key, sehingga yang terhapus selalu leaf node.
c1) Untuk 2-3 Tree:
- Jika leaf 3-node, langsung delete targeted key dan menjadi 2-node.
- Jika leaf 2-node:
+ Jika parentnya 3-node, ambil 1 value dari node tersebut. Jika siblingnya adalah 3-node, maka push satu value dari siblingnya ke parent. Jika siblingnya 2-node, buat parent 2-node dan merge node sekarang dengan siblingnya.
+ Jika parentnya 2-node, jika sibling 3-node maka ambil satu value dari parent dan push 1 value dari siblingnya ke parent. Jika sibling 2-node, merge parent dengan siblingnya.
c2) Untuk m-Tree:
- Simbolkan leaf node yang mereplace targeted key adalah p.
- Jika p > m/2, maka langsung delete.
- Jika p == m/2: Cek sibling (q).
+ Jika q > m/2, maka rotate value ke p (melalui parentnya)
+ Jika q == m/2, merge p dan q (dan 1 key dari parentnya)
d) Perbaiki parent secara rekursif.
Contoh:
RED BLACK TREE
Sifat Red-Black Tree
1. Tiap node memiliki warna, antara merah atau hitam.
2. Root berwarna hitam secara default.
3. Semua node eksternal adalah hitam.
4. Jika node merah, maka kedua childrennya hitam. (Tidak ada node merah yang memiliki parent merah)
Insertion Red-Black Tree
a) Masukkan value sesuai prosedur BST (kecil ke kiri, besar ke kanan), posisi akan berada di leaf node.
b) New node adalah merah.
c) Jika parent hitam, no violation. Jika parent merah, violation terjadi.
Langkah Perbaiki Violation
Pemisalan: node => q, parent => p, uncle => s
Jika s merah, ubah p dan s menjadi hitam dan grandparent menjadi merah.
Jika s hitam, lakukan rotasi (single atau double), ubah pivot terakhir menjadi hitam dan anak menjadi merah.
Deletion Red-Black Tree
a) Menentukan target deleted node, lalu mencari leaf node (kiri terbesar atau kanan terkecil) yang mereplace deleted node, lalu hapus leaf nodenya.
b) Pemisalan: node yang didelete => M, child node => C
c1) Jika M merah, langsung replace saja dengan C.
c2) Jika M hitam dan C merah, maka replace dengan C dan recolor C dengan hitam.
c3) Jika M dan C hitam (doubleblack), maka replace M dengan C, lalu cek:
doubleblack => DB, parent => P, sibling => S, sibling's left child => Sl, sibling's right child => Sr
- Jika S merah, tukar warna DB dan P, lalu rotate di P. => recheck DB
- Jika S, Sl, dan Sr hitam, recolor S merah. => recheck DB
- Jika S hitam dan Sl atau Sr merah, maka lakukan single atau double rotation, lalu ubah child menjadi hitam => remove DB
d) Lakukan pengecekan doubleblack hingga hilang.
Kak Dwi. Berikut ini rangkuman materi pembahasan mengenai heaps dan tries yang disampaikan dosen tamu.
HEAPS
Heap merupakan pengembangan konsep berdasarkan struktur data Binary Search Tree Complete dengan memenuhi sifat heap.
Konsep heap terdiri dari 3 bentuk:
A. Min Heap
IMPLEMENTASI ARRAY DALAM HEAPS
Heap bisa diimplementasikan menggunakan linked list, namun akan jauh lebih mudah jika menggunakan array.
Index array root dimulai dari 1 (bukan 0, dijelaskan di bawah) hingga ke N karena terkait dengan rumus menemukan root.
Cara menggunakan array untuk heaps adalah:
- Index 1 selalu rootnya, dalam contoh ini menggunakan min heap, maka valuenya yang paling kecil, yaitu 7.
- Index berikutnya bergerak maju sejajar mengisi children nodesnya hingga full lalu turun lagi, dst. (Mulai dari kiri ke kanan sampai semua leaf node terisi).
Node yang memiliki relasi dengan parent, left child, dan right child yang menggunakan implementasi array akan lebih mudah diolah.
Cara menemukan index, dengan pemisalahan index node sekarang adalah x:
a. Parent (x) = x/2
b. Left Child (x) = 2 * x
c. Right Child (x) = 2 * x + 1
Misalkan dengan contoh gambar di atas:
Index array [1] = 7, [2] = 15, [4] = 30, [5] = 31
Misalkan current node adalah value 15, ada di index 2.
- Menemukan index parentnya = x/2 = 2/2 = 1, yaitu value 7.
- Menemukan index left child = 2 * x = 2 * 2 = 4, yaitu value 30.
Kenapa value 30 di index 4, karena penyusunan heap sudah pasti mengisi jajaran node hingga full (untuk di height 2 maka harusnya ada 2 node, supaya di height 3 boleh diisi).
- Menemukan index right child = 2 * x + 1 = 2 * 2 + 1 = 5, yaitu value 31.
Dari contoh ilustrasi di atas, maka kita bisa menjawab alasan kenapa root harus index 1. Karena rumus parent(2) = 2/2 = 1 untuk mencapai root dalam kasus contoh di atas. Jika root dimasukkan ke index 0, maka tidak akan akan bisa ditemukan dengan rumus.
MENEMUKAN VALUE TERKECIL DI MIN HEAP
Menemukan value terkecil di min heap sangatlah mudah karena nilai terkecil pasti ada di rootnya yang dimana kita tinggal me-return data[1].
INSERTION DI MIN HEAP
Langkah:
- Memasukkan elemen baru ke node paling bawah kanan yang kosong, atau jika sudah full, masukkan ke child baru paling kiri. (Setelah index dari elemen terakhir).
- Perbaiki struktur dengan konsep upheap terhadap elemen baru tersebut (Memperbaiki sifat heap).
a) Membandingkan current node (mulai dari value node yang baru dimasukkan) dengan value parentnya. Jika value current node lebih kecil dari value parent, maka lakukan swap. Lalu, teruskan upheap parent nodenya.
b) Berhenti jika value current node lebih besar dari value parent atau current nodenya adalah root (tidak ada parent lagi).
Contohnya:
Dimasukkan value baru yaitu 20. Node baru ini diletakkan ke paling bawah kanan setelah index elemen terakhir yaitu sebelah kanan node value 32. Lalu, cek value current node dengan value parent, ternyata 20 < 28, maka swap sehingga posisi parent yang awalnya berisi 28 menjadi 20 dan 28 turun menjadi child dari 20. Lalu, cek lagi ke parentnya yaitu 15, ternyata 20 > 15, maka berhenti.
Contoh lain:
Dimasukkan value baru 5, posisinya paling bawah kanan sebelah value 28. Cek current node dengan parent, ternyata 5 < 17, maka swap, sehingga value di parent yg awalnya 17 menjadi 5 (dan sekarang menjadi current node) dan 17 turun menjadi child.
Lalu, cek lagi current node dengan parent, ternyata 5 < 10, maka swap, sehingga value di parent awalnya 10 menjadi 5 (sekarang jadi current node) dan value 10 menjadi child node dari value 5. Cek lagi ternyaa 5 < 7, maka swap sehingga angka 5 menjadi root (current node) dan sudah paling atas, maka berhenti.
DELETION DI MIN HEAP
Langkah:
- Delete selalu dilakukan paling atas (pada bagian root).
- Replace root dengan elemen terakhir heap.
- Kurangi jumlah elemen heap
- Perbaiki struktur dengan konsep downheap sesuai dengan sifat heap.
a) Bandingkan value current node (mulai dari root) dengan value left child dan right child. Jika ada value child (paling kecil) < current node, maka swap, lalu cek lagi ke bawah.
b) Berhenti jika value current node < value child kiri dan kanan atau current node adalah leaf node. (Tidak memiliki child nodes lagi).
Contohnya:
B. Max Heap
Langkah:
- Memasukkan elemen baru ke node paling bawah kanan yang kosong, atau jika sudah full, masukkan ke child baru paling kiri. (Setelah index dari elemen terakhir).
- Perbaiki struktur dengan konsep upheap terhadap elemen baru tersebut (Memperbaiki sifat heap).
a) Membandingkan current node (mulai dari value node yang baru dimasukkan) dengan value parentnya. Jika value current node lebih besar dari value parent, maka lakukan swap. Lalu, teruskan upheap parent nodenya.
b) Berhenti jika value current node lebih kecil dari value parent atau current nodenya adalah root (tidak ada parent lagi).
DELETION DI MAX HEAP
Langkah:
- Delete selalu dilakukan paling atas (pada bagian root).
- Replace root dengan elemen terakhir heap.
- Kurangi jumlah elemen heap
- Perbaiki struktur dengan konsep downheap sesuai dengan sifat heap.
a) Bandingkan value current node (mulai dari root) dengan value left child dan right child. Jika ada value child (paling besar) > current node, maka swap, lalu cek lagi ke bawah.
b) Berhenti jika value current node > value child kiri dan kanan atau current node adalah leaf node. (Tidak memiliki child nodes lagi).
C. Min-Max Heap
MENEMUKAN VALUE TERBESAR DI MIN_MAX HEAP
Value terbesar pasti berada di children node dari root yaitu pada level 2 antara pada child kiri atau child kanan yang memiliki value terbesar, dengan return max(data[2], data[3]).
#Value terbesar bisa terletak di root jika heap hanya memiliki 1 data.
INSERTION DI MIN-MAX HEAP
Langkah:
- Memasukkan elemen baru ke node paling bawah kanan yang kosong, atau jika sudah full, masukkan ke child baru paling kiri. (Setelah index dari elemen terakhir).
- Perbaiki struktur dengan konsep upheap terhadap elemen baru tersebut (Memperbaiki sifat heap).
a) Jika node baru berada di level min:
* Jika parent < current node, lakukan swap, dan upheapmax dari parentnya.
* Jika parent > current node, lakukan upheapmin dari current node.
b) Jika node baru berada di level max:
* Jika parent > current node, maka lakukan swap, dan upheapmin dari parentnya.
* Jika parent < current node, maka lakukan upheapmax dari current node.
UPHEAPMIN DI MIN-MAX HEAP
Bandingkan value current node dengan value grandparentnya.
Jika value current node < value parent, lakukan swap value, lanjutkan upheapmin grandparent nodenya.
UPHEAPMAX DI MIN-MAX HEAP
Bandingkan value current node dengan value grandparentnya.
Jika value current node > value parent, lakukan swap value, lanjutkan upheapmax grandparent nodenya.
#Intinya, kalau current node maka cek parentnya sesuai kriteria parentnya berada di level tertentu (min/max).
Jika di level min, maka cek apakah value current node lebih kecil dari value parent, jika ya maka swap, jika tidak maka naik lagi ke grandparent (lakukan validasi sesuai min level), dan lakukan hal yang sama secara rekursif hingga ke root.
Jika di level max, maka cek apakah value current node lebih besar dari value parent, jika ya maka swap, jika tidak maka naik lagi ke grandparent (lakukan validasi sesuai maxlevel), lakukan hal yang sama secara rekursif hingga ke root.
CONTOH INSERTION MIN-MAX HEAP
Contoh 1:
Ada insertion value 50, berada di level max. Cek parent dengan current node, ternyata 28 < 50, maka lakukan upheapmax (naik lagi). Cek grandparent, ternyata value grandparent (35) < value current node (50), maka dilakukan swap value dan current node sekarang berada di tempat grandparent.
Lanjut cek parent (min level) dengan current node (max level), 8 < 50, maka cek upheap max namun karena node value 50 tidak memiliki grandparent, maka proses selesai.
Contoh 2:
Ada insertion value 5 di level max. Cek parentnya (14, level min). Ternyata 5 < 14, maka swap valuenya sehingga current node sekarang adalah 5 yang posisinya di parent.
Cek lagi current node (5, min level) dengan parentnya (27, max level). Ternyata 14 < 27, maka cek grandparent (8, min level) dengan current node (5, min level). Ternyata 8 > 5, maka lakukan swap value dan berhenti karena sudah sampai root. Maka hasilnya menjadi:
DELETION DI MIN-MAX HEAP
a) Deletion Value Terkecil
- Replace value root dengan elemen terakhir di heap.
- Mengurangi jumlah elemen di heap.
- Downheapmin dari rootnya.
b) Deletion Value Terbesar
- Mereplace antara anak kiri atau anak kanan dari root (yang nilainya paling besar) dengan elemen terakhir di heap dan akan menjadi current node.
- Kurangi jumlah elemen di heap / hapus index terakhir.
- Downheapmax dari current node
DOWNHEAPMIN DI MIN-MAX HEAP
Misalkan m adalah elemen terkecil di anak current node dan grandchildren (jika ada).
Jika m adalah grandchildren dari current node maka:
- Jika m lebih kecil current node:
* swap valuenya.
* Jika m lebih besar dari parent swap valuenya.
* Lanjutkan downheapmin dari m.
- Jika m adalah anak dari current node maka:
* Jika m lebih kecil dari current node maka swap value.
DOWNHEAPMAX DI MIN-MAX HEAP
Misalkan m adalah elemen terbesar di child current node dan grandchildren (jika ada).
= Jika m adalah grandchildren dari current node maka:
- Jika m lebih besar dari current node:
* swap valuenya.
* Jika m lebih kecil dari parent swap valuenya.
* Lanjutkan downheapmax dari m.
= Jika m adalah anak dari current node maka:
* Jika m lebih besar dari current node maka swap value.
CONTOH DELETION MIN-MAX HEAP
Contoh delete max:
Value paling besar ada di child kiri node yaitu 50, maka ganti 50 dengan elemen terakhir yaitu 14 dan delete leaf node 14. Lalu lakukan downheapmax.
Sekarang current node ada di value 14. Elemen terbesar dari child dan grandchildren adalah 35, yaitu grandchild kanan dari child kanan, maka cek apakah value 35 > 14, maka swap valuenya.
Lalu cek ternyata value grandchild kanan (14) < value parentnya (28), maka swap valuenya. Lanjutkan downheapmax.
Current node sekarang value 28. Karena 28 tidak memiliki children atau grandchildren, maka proses selesai.
APPLICATION OF HEAPS
CONCEPT OF TRIES
Tries adalah tree data structure yang sudah terorder yang digunakan untuk menyimpan array asosiatif (biasanya berupa strings). Tries adalah tree dimana tiap vertex mewakili satu kata atau prefix.
Root tries selalu berupa empty character ('') dengan tujuan agar tidak hanya berfokus pada 1 karakter saja. Misalnya jika root dimasukkan huruf 'P', maka hanya bisa membuat kata dengan awalan huruf 'P'.
Penggunaan konsep tries ini bisa ditemukan di aplikasi yang menyimpan data kata (misalnya, daftar kata di KBBI) yang biasa ditemukan pada web browser untuk fitur auto complete text, spell checker untuk mendeteksi tiap huruf dan melakukan koreksi kata, dan masih banyak lagi.
Konsep tries ini dapat memiliki banyak cabang sesuai dengan padanan kata. Contohnya, pada contoh di atas, rootnya adalah empty character. Kemudian ada children node 'B', 'S', dan 'A'.
Dari char 'B' tidak bisa membentuk kata.
Dari char 'S' bisa membentuk kata speak, speaker, spa, space, spaceship, spade.
Dari char 'A' bisa membentuk kata and.
Jika melihat contoh untuk character 'S' maka ada beberapa kata yang tergabung dalam satu susunan, maka pemberian tanda khusus bisa memberi hint batas akhir dari sebuah kata.
SPEAK (PEMBATAS), SPEAKER (PEMBATAS) atau
SPA (PEMBATAS), SPACE (PEMBATAS), SPACESHIP (PEMBATAS) atau SPADE (PEMBATAS).
Himpunan adalah kumpulan dari objek.
Himpunan A adalah subset himpunan B jika semua elemen di A ada di B.
Gabungan dari himpunan A dan B adalah himpunan C yang mengandung semua elemen di A dan B.
Dua himpunan disjoint jika mereka tidak memiliki elemen umum yang sama.
Partisi adalah pembagian satu set ke banyak kelompok berdasarkan pada relasi ekuivalensi.
Contoh:
S = {1,2,3,4}; A = {1,2}; B = {3,4}; C = {2,3,4}; D = {4}
A,B adalah partisi dari S.
A,C bukan partisi dari S.
A, D bukan partisi dari S.
Disjoint Sets
Disjoint set, dikenal juga 'Union-Find', berbeda dengan set.
Disjoint set adalah struktur data yang melacak sekumpulan elemen yang dipartisi menjadi sejumlah subset disjoint (non-overlapping).
Disjoint Set dapat digunakan untuk menentukan siklus dalam grafik, yang membantu dalam menemukan pohon spanning minimum grafik (MST).
Operasi Disjoint Sets
1) makeSet(x)
- Untuk membuat himpunan baru yang mengandung elemen x.
- Sebuah himpunan yang hanya memiliki 1 elemen disebut himpunan singleton.
- Awalnya akan ada pointer menuju diri sendiri (looping).
2) findSet(x)
- Operasi yang mengembalikan perwakilan himpunan dimana x terletak di himpunan tersebut.
- Berguna untuk cek apakah elemen milik sebuah set.
3) union(x,y)
- Membuat himpunan baru yang mengandung elemen-elemen dari humpunan x dan y, kemudian menghapus himpunan tersendiri dari x dan y.
- Dua himpunan bisa di-merge dengan membuat root dari satu himpunan menunjuk ke root dari himpunan lain.
Path Compression
Path Compression adalah teknik yang digunakan untuk meningkatkan efisiensi operasi find (untuk meningkatkan kinerja operasi find, setiap node harus memiliki pointer langsung ke root).
Algoritma bekerja dengan memeriksa apakah node sudah di-root, maka tidak perlu dilakukan. Jika tidak, pointer harus diperbarui untuk menunjuk ke root.
Graphs
Grafik adalah struktur data abstrak yang digunakan untuk mengimplementasikan konsep matematika grafik. Pada dasarnya, grafik adalah kumpulan vertices (juga disebut node/simpul) dan edges yang menghubungkan simpul-simpul ini.
Grafik dapat membantu kita dalam mentransformasikan data yang terkait satu sama lain. E. g. Maps, Family Tree, Obrolan Obrolan Game, dll.
Undirected Graph: Graph tanpa tanda panah, bisa diakses 2 arah.
Directed Graph: Graph dengan arah tanda panah.
Ada in-degree (semua garis yang masuk ke vertex).
Ada out-degree (semua garis yang keluar dari vertex).
Adjacency List Matrix
Merupakan cara menjabarkan jumlah degree yang menghubungkan 2 vertex dalam bentuk matrix, bisa juga dibuat dalam bentuk array dan linked-list.
MST - Prim's Algorithm
Penjelasan:
1. Buat array dengan nama adalah T.
2. Pilih titik awal vertex.
3. Setiap kali setiap vertex ditunjuk, edge yang terhubung akan aktif.
4. Bandingkan semua nilai edges aktif, temukan angka terkecil.
5. Tambahkan node dengan tepi aktif terkecil ke T.
6. Lakukan langkah 3 hingga 5 sementara simpul dalam T lebih sedikit dari total simpul yang ada.
Contoh:
- Pilih vertex awal (A). Masukkan semua edge yang berhubungan dengan vertex A ke dalam Priority Queue berdasarkan cost. Pilih (dengan coret) edge paling atas.
- Lanjut ke vertex yang menjadi pasangan di edge yang dicoret, yaitu C. Tambahkan semua edge yg berhubungan dengan vertex C ke dalam Priority Queue berdasarkan costnya. Coret edge paling atas.
- Lanjut lagi melakukan prinsip langkah yang sama.
MST - Kruskal's Algorithm
Penjelasan:
1. Buat array dengan nama adalah T.
2. Urutkan semua edges menggunakan heap (Priority Queue, langsung dari awal)
3. Ambil nilai edge paling minimum
4a. Jika ada loop (ada jalur bisa ke vertex, bagaimanapun caranya), lanjutkan ke edge berikutnya/tolak.
4b. Jika tidak, maka menambahkan edge ke T/terima.
5. Ulangi langkah 3 hingga 5 hingga semua vertex dikunjungi
Contoh:
Sort langsung semua edges dari cost terkecil ke terbesar. Cek secara berurutan apakah sudah ada jalur yang menghubungkan kedua vertex dengan current edges (bagaimanapun jalur/caranya).
a) Jika ada jalur yang menghubungkan, tolak (continue).
b) Jika belum ada jalur, terima, masukkan ke T.
Stop jika semua vertex sudah dilewati (Jumlah edges di T jumlahnya sudah jumlah vertex-1).
Shortest Path - Djikstra's Algorithm
Shortest Path adalah metode yang digunakan untuk menemukan jalur terpendek dari graph dengan vertex awal dan akhir yang spesifik. Bisa dicari dengan menggunakan Algoritma Djikstra.
Penjelasan:
1. Pilih simpul sumber (simpul awal)
2. Tentukan N sebagai set kosong
3. Beri label simpul awal dengan 0, dan masukkan ke dalam N
4. Ulangi langkah 5 hingga 7 hingga simpul tujuan berada di N atau tidak ada mode berlabel node di N.
5. Pertimbangkan setiap simpul yang tidak dalam N dan terhubung oleh tepi dari simpul yang baru dimasukkan.
6.
a) Jika node yang tidak dalam N tidak memiliki label maka SET label label = label dari node yang baru dimasukkan + panjang tepi
b) Jika node yang tidak dalam N sudah diberi label, maka SET label baru = minimum (label titik baru dimasukkan + panjang tepi, label lama)
7. Pilih satu simpul yang bukan di N yang memiliki label terkecil yang ditugaskan padanya dan tambahkan ke N.
Contoh:
Demikian materi data structure yang saya pelajari di semester 2 ini. Mohon maaf jika ada kekurangan atau kesalahan. Terima kasih terkhusus pada dosen Pak Henry dan Pak Ferdinand yang telah memberikan ilmu kepada saya dan mahasiswa fakultas Teknik Informatika.
Angelia
2301854492
Hari: Senin, 15/06/2020
Kelas: CB01
Lecturer:
Referensi:
PPT Binus Maya
Zoom Meeting
Link web belajar lainnya
b) Pemisalan: node yang didelete => M, child node => C
c1) Jika M merah, langsung replace saja dengan C.
c2) Jika M hitam dan C merah, maka replace dengan C dan recolor C dengan hitam.
c3) Jika M dan C hitam (doubleblack), maka replace M dengan C, lalu cek:
doubleblack => DB, parent => P, sibling => S, sibling's left child => Sl, sibling's right child => Sr
- Jika S merah, tukar warna DB dan P, lalu rotate di P. => recheck DB
- Jika S, Sl, dan Sr hitam, recolor S merah. => recheck DB
- Jika S hitam dan Sl atau Sr merah, maka lakukan single atau double rotation, lalu ubah child menjadi hitam => remove DB
d) Lakukan pengecekan doubleblack hingga hilang.
HEAPS & TRIES
Pada pertemuan sesi ke-11, dilakukan video conference dengan dosen tamu yang dibawakan olehKak Dwi. Berikut ini rangkuman materi pembahasan mengenai heaps dan tries yang disampaikan dosen tamu.
HEAPS
Heap merupakan pengembangan konsep berdasarkan struktur data Binary Search Tree Complete dengan memenuhi sifat heap.
Konsep heap terdiri dari 3 bentuk:
A. Min Heap
Konsep min heap adalah bahwa node parent memiliki value paling kecil daripada node childrennya. Hal ini menyimpulkan bahwa value terkecil akan terletak di root tree nya.
IMPLEMENTASI HEAP UNTUK PRIORITY QUEUE
Heap dapat menjadi implementasi priority queue yang efisien.
* mencari minimum = menemukan value terkecil di heap.
* insert/push = insert elemen baru ke dalam heap.
* delete/pop minimum = delete value paling kecil di heap.
IMPLEMENTASI ARRAY DALAM HEAPS
Heap bisa diimplementasikan menggunakan linked list, namun akan jauh lebih mudah jika menggunakan array.
Index array root dimulai dari 1 (bukan 0, dijelaskan di bawah) hingga ke N karena terkait dengan rumus menemukan root.
Cara menggunakan array untuk heaps adalah:
- Index 1 selalu rootnya, dalam contoh ini menggunakan min heap, maka valuenya yang paling kecil, yaitu 7.
- Index berikutnya bergerak maju sejajar mengisi children nodesnya hingga full lalu turun lagi, dst. (Mulai dari kiri ke kanan sampai semua leaf node terisi).
Node yang memiliki relasi dengan parent, left child, dan right child yang menggunakan implementasi array akan lebih mudah diolah.
a. Parent (x) = x/2
b. Left Child (x) = 2 * x
c. Right Child (x) = 2 * x + 1
Misalkan dengan contoh gambar di atas:
Index array [1] = 7, [2] = 15, [4] = 30, [5] = 31
Misalkan current node adalah value 15, ada di index 2.
- Menemukan index parentnya = x/2 = 2/2 = 1, yaitu value 7.
- Menemukan index left child = 2 * x = 2 * 2 = 4, yaitu value 30.
Kenapa value 30 di index 4, karena penyusunan heap sudah pasti mengisi jajaran node hingga full (untuk di height 2 maka harusnya ada 2 node, supaya di height 3 boleh diisi).
- Menemukan index right child = 2 * x + 1 = 2 * 2 + 1 = 5, yaitu value 31.
Dari contoh ilustrasi di atas, maka kita bisa menjawab alasan kenapa root harus index 1. Karena rumus parent(2) = 2/2 = 1 untuk mencapai root dalam kasus contoh di atas. Jika root dimasukkan ke index 0, maka tidak akan akan bisa ditemukan dengan rumus.
MENEMUKAN VALUE TERKECIL DI MIN HEAP
Menemukan value terkecil di min heap sangatlah mudah karena nilai terkecil pasti ada di rootnya yang dimana kita tinggal me-return data[1].
INSERTION DI MIN HEAP
Langkah:
- Memasukkan elemen baru ke node paling bawah kanan yang kosong, atau jika sudah full, masukkan ke child baru paling kiri. (Setelah index dari elemen terakhir).
- Perbaiki struktur dengan konsep upheap terhadap elemen baru tersebut (Memperbaiki sifat heap).
a) Membandingkan current node (mulai dari value node yang baru dimasukkan) dengan value parentnya. Jika value current node lebih kecil dari value parent, maka lakukan swap. Lalu, teruskan upheap parent nodenya.
b) Berhenti jika value current node lebih besar dari value parent atau current nodenya adalah root (tidak ada parent lagi).
Contohnya:
Contoh lain:
DELETION DI MIN HEAP
Langkah:
- Delete selalu dilakukan paling atas (pada bagian root).
- Replace root dengan elemen terakhir heap.
- Kurangi jumlah elemen heap
- Perbaiki struktur dengan konsep downheap sesuai dengan sifat heap.
a) Bandingkan value current node (mulai dari root) dengan value left child dan right child. Jika ada value child (paling kecil) < current node, maka swap, lalu cek lagi ke bawah.
b) Berhenti jika value current node < value child kiri dan kanan atau current node adalah leaf node. (Tidak memiliki child nodes lagi).
Contohnya:
Dilakukan deletion pertama yaitu value 7 yang ada di root. Maka ganti value root dengan value node paling kanan bawah atau node elemen paling terakhir, yaitu 28. Maka value root sekarang adalah 28, dan node elemen terakhir bisa dihapus. Kemudian, cek anak kiri dan kanan, ternyata value paling kecil ada di child kanan (10<15<28), maka swap value root dengan value child kanan sehingga current node sekarang di child kanan dengan value 28.
Lanjut cek ke bawah, antara current node dengan left dan right child, ternyata RC (12) < LF (17) < P (28), maka swap right child dengan parent sehingga value right child sekarang menjadi 28 dan parentnya menjadi 12. Ketika hendak dilanjut cek ke bawah, ternyata node value 28 sudah merupakan leaf node, sehingga berhenti.
B. Max Heap
Konsep max heap adalah bahwa node parent memiliki value paling besar daripada node childrennya.
Jadi, value terbesar berada di root heapnya.
IMPLEMENTASI HEAP UNTUK PRIORITY QUEUE
Heap dapat menjadi implementasi priority queue yang efisien.
* mencari max= menemukan value terbesar di heap.
* insert/push = insert elemen baru ke dalam heap.
* delete/pop max= delete value paling besar di heap.
Prinsip insertion dan deletion mirip dengan min heap.
INSERTION DI MAX HEAPLangkah:
- Memasukkan elemen baru ke node paling bawah kanan yang kosong, atau jika sudah full, masukkan ke child baru paling kiri. (Setelah index dari elemen terakhir).
- Perbaiki struktur dengan konsep upheap terhadap elemen baru tersebut (Memperbaiki sifat heap).
a) Membandingkan current node (mulai dari value node yang baru dimasukkan) dengan value parentnya. Jika value current node lebih besar dari value parent, maka lakukan swap. Lalu, teruskan upheap parent nodenya.
b) Berhenti jika value current node lebih kecil dari value parent atau current nodenya adalah root (tidak ada parent lagi).
DELETION DI MAX HEAP
Langkah:
- Delete selalu dilakukan paling atas (pada bagian root).
- Replace root dengan elemen terakhir heap.
- Kurangi jumlah elemen heap
- Perbaiki struktur dengan konsep downheap sesuai dengan sifat heap.
a) Bandingkan value current node (mulai dari root) dengan value left child dan right child. Jika ada value child (paling besar) > current node, maka swap, lalu cek lagi ke bawah.
b) Berhenti jika value current node > value child kiri dan kanan atau current node adalah leaf node. (Tidak memiliki child nodes lagi).
C. Min-Max Heap
Konsep min-max heap adalah bahwa untuk height awal pasti menggunakan konsep min heap dimana node valuenya paling kecil dibanding childrennya, lalu di height ke-2 menggunakan konsep max heap dimana value node paling besar dibanding childrennya, dan berlanjut terus menggunakan konsep heap secara bergantian.
Kondisi heap pada bentuk ini memiliki 2 bentuk antara minimum dan maximum.
- Tiap elemen di level ganjil/genap lebih kecil dari semua anaknya (min level).
- Tiap elemen di level ganjil/genap lebih besar dari semua anaknya (max level).
Tujuan min-max heap adalah untuk mempermudah kita mencari nilai terkecil dan terbesar dalam heap di waktu yang bersamaan.
MENEMUKAN VALUE TERKECIL DI MIN-MAX HEAP
Value terkecil di heap pasti berada di level 0 atau di root, dengan return data[1].
Value terbesar pasti berada di children node dari root yaitu pada level 2 antara pada child kiri atau child kanan yang memiliki value terbesar, dengan return max(data[2], data[3]).
#Value terbesar bisa terletak di root jika heap hanya memiliki 1 data.
INSERTION DI MIN-MAX HEAP
Langkah:
- Memasukkan elemen baru ke node paling bawah kanan yang kosong, atau jika sudah full, masukkan ke child baru paling kiri. (Setelah index dari elemen terakhir).
- Perbaiki struktur dengan konsep upheap terhadap elemen baru tersebut (Memperbaiki sifat heap).
a) Jika node baru berada di level min:
* Jika parent < current node, lakukan swap, dan upheapmax dari parentnya.
* Jika parent > current node, lakukan upheapmin dari current node.
b) Jika node baru berada di level max:
* Jika parent > current node, maka lakukan swap, dan upheapmin dari parentnya.
* Jika parent < current node, maka lakukan upheapmax dari current node.
UPHEAPMIN DI MIN-MAX HEAP
Bandingkan value current node dengan value grandparentnya.
Jika value current node < value parent, lakukan swap value, lanjutkan upheapmin grandparent nodenya.
UPHEAPMAX DI MIN-MAX HEAP
Bandingkan value current node dengan value grandparentnya.
Jika value current node > value parent, lakukan swap value, lanjutkan upheapmax grandparent nodenya.
#Intinya, kalau current node maka cek parentnya sesuai kriteria parentnya berada di level tertentu (min/max).
Jika di level min, maka cek apakah value current node lebih kecil dari value parent, jika ya maka swap, jika tidak maka naik lagi ke grandparent (lakukan validasi sesuai min level), dan lakukan hal yang sama secara rekursif hingga ke root.
Jika di level max, maka cek apakah value current node lebih besar dari value parent, jika ya maka swap, jika tidak maka naik lagi ke grandparent (lakukan validasi sesuai maxlevel), lakukan hal yang sama secara rekursif hingga ke root.
CONTOH INSERTION MIN-MAX HEAP
Contoh 1:
Contoh 2:
DELETION DI MIN-MAX HEAP
a) Deletion Value Terkecil
- Replace value root dengan elemen terakhir di heap.
- Mengurangi jumlah elemen di heap.
- Downheapmin dari rootnya.
b) Deletion Value Terbesar
- Mereplace antara anak kiri atau anak kanan dari root (yang nilainya paling besar) dengan elemen terakhir di heap dan akan menjadi current node.
- Kurangi jumlah elemen di heap / hapus index terakhir.
- Downheapmax dari current node
DOWNHEAPMIN DI MIN-MAX HEAP
Misalkan m adalah elemen terkecil di anak current node dan grandchildren (jika ada).
Jika m adalah grandchildren dari current node maka:
- Jika m lebih kecil current node:
* swap valuenya.
* Jika m lebih besar dari parent swap valuenya.
* Lanjutkan downheapmin dari m.
- Jika m adalah anak dari current node maka:
* Jika m lebih kecil dari current node maka swap value.
DOWNHEAPMAX DI MIN-MAX HEAP
Misalkan m adalah elemen terbesar di child current node dan grandchildren (jika ada).
= Jika m adalah grandchildren dari current node maka:
- Jika m lebih besar dari current node:
* swap valuenya.
* Jika m lebih kecil dari parent swap valuenya.
* Lanjutkan downheapmax dari m.
= Jika m adalah anak dari current node maka:
* Jika m lebih besar dari current node maka swap value.
CONTOH DELETION MIN-MAX HEAP
Contoh delete max:
APPLICATION OF HEAPS
CONCEPT OF TRIES
Tries adalah tree data structure yang sudah terorder yang digunakan untuk menyimpan array asosiatif (biasanya berupa strings). Tries adalah tree dimana tiap vertex mewakili satu kata atau prefix.
Root tries selalu berupa empty character ('') dengan tujuan agar tidak hanya berfokus pada 1 karakter saja. Misalnya jika root dimasukkan huruf 'P', maka hanya bisa membuat kata dengan awalan huruf 'P'.
Penggunaan konsep tries ini bisa ditemukan di aplikasi yang menyimpan data kata (misalnya, daftar kata di KBBI) yang biasa ditemukan pada web browser untuk fitur auto complete text, spell checker untuk mendeteksi tiap huruf dan melakukan koreksi kata, dan masih banyak lagi.
Konsep tries ini dapat memiliki banyak cabang sesuai dengan padanan kata. Contohnya, pada contoh di atas, rootnya adalah empty character. Kemudian ada children node 'B', 'S', dan 'A'.
Dari char 'B' tidak bisa membentuk kata.
Dari char 'S' bisa membentuk kata speak, speaker, spa, space, spaceship, spade.
Dari char 'A' bisa membentuk kata and.
Jika melihat contoh untuk character 'S' maka ada beberapa kata yang tergabung dalam satu susunan, maka pemberian tanda khusus bisa memberi hint batas akhir dari sebuah kata.
SPEAK (PEMBATAS), SPEAKER (PEMBATAS) atau
SPA (PEMBATAS), SPACE (PEMBATAS), SPACESHIP (PEMBATAS) atau SPADE (PEMBATAS).
DISJOINT SETS & GRAPHS
HimpunanHimpunan adalah kumpulan dari objek.
Himpunan A adalah subset himpunan B jika semua elemen di A ada di B.
Gabungan dari himpunan A dan B adalah himpunan C yang mengandung semua elemen di A dan B.
Dua himpunan disjoint jika mereka tidak memiliki elemen umum yang sama.
Partisi adalah pembagian satu set ke banyak kelompok berdasarkan pada relasi ekuivalensi.
Contoh:
S = {1,2,3,4}; A = {1,2}; B = {3,4}; C = {2,3,4}; D = {4}
A,B adalah partisi dari S.
A,C bukan partisi dari S.
A, D bukan partisi dari S.
Disjoint Sets
Disjoint set, dikenal juga 'Union-Find', berbeda dengan set.
Disjoint set adalah struktur data yang melacak sekumpulan elemen yang dipartisi menjadi sejumlah subset disjoint (non-overlapping).
Disjoint Set dapat digunakan untuk menentukan siklus dalam grafik, yang membantu dalam menemukan pohon spanning minimum grafik (MST).
Operasi Disjoint Sets
1) makeSet(x)
- Untuk membuat himpunan baru yang mengandung elemen x.
- Sebuah himpunan yang hanya memiliki 1 elemen disebut himpunan singleton.
- Awalnya akan ada pointer menuju diri sendiri (looping).
2) findSet(x)
- Operasi yang mengembalikan perwakilan himpunan dimana x terletak di himpunan tersebut.
- Berguna untuk cek apakah elemen milik sebuah set.
3) union(x,y)
- Membuat himpunan baru yang mengandung elemen-elemen dari humpunan x dan y, kemudian menghapus himpunan tersendiri dari x dan y.
- Dua himpunan bisa di-merge dengan membuat root dari satu himpunan menunjuk ke root dari himpunan lain.
Path Compression
Path Compression adalah teknik yang digunakan untuk meningkatkan efisiensi operasi find (untuk meningkatkan kinerja operasi find, setiap node harus memiliki pointer langsung ke root).
Algoritma bekerja dengan memeriksa apakah node sudah di-root, maka tidak perlu dilakukan. Jika tidak, pointer harus diperbarui untuk menunjuk ke root.
Graphs
Grafik adalah struktur data abstrak yang digunakan untuk mengimplementasikan konsep matematika grafik. Pada dasarnya, grafik adalah kumpulan vertices (juga disebut node/simpul) dan edges yang menghubungkan simpul-simpul ini.
Grafik dapat membantu kita dalam mentransformasikan data yang terkait satu sama lain. E. g. Maps, Family Tree, Obrolan Obrolan Game, dll.
Undirected Graph: Graph tanpa tanda panah, bisa diakses 2 arah.
Directed Graph: Graph dengan arah tanda panah.
Ada in-degree (semua garis yang masuk ke vertex).
Ada out-degree (semua garis yang keluar dari vertex).
Adjacency List Matrix
Merupakan cara menjabarkan jumlah degree yang menghubungkan 2 vertex dalam bentuk matrix, bisa juga dibuat dalam bentuk array dan linked-list.
MST - Prim's Algorithm
Penjelasan:
1. Buat array dengan nama adalah T.
2. Pilih titik awal vertex.
3. Setiap kali setiap vertex ditunjuk, edge yang terhubung akan aktif.
4. Bandingkan semua nilai edges aktif, temukan angka terkecil.
5. Tambahkan node dengan tepi aktif terkecil ke T.
6. Lakukan langkah 3 hingga 5 sementara simpul dalam T lebih sedikit dari total simpul yang ada.
Contoh:
- Lanjut ke vertex yang menjadi pasangan di edge yang dicoret, yaitu C. Tambahkan semua edge yg berhubungan dengan vertex C ke dalam Priority Queue berdasarkan costnya. Coret edge paling atas.
- Lanjut lagi melakukan prinsip langkah yang sama.
MST - Kruskal's Algorithm
Penjelasan:
1. Buat array dengan nama adalah T.
2. Urutkan semua edges menggunakan heap (Priority Queue, langsung dari awal)
3. Ambil nilai edge paling minimum
4a. Jika ada loop (ada jalur bisa ke vertex, bagaimanapun caranya), lanjutkan ke edge berikutnya/tolak.
4b. Jika tidak, maka menambahkan edge ke T/terima.
5. Ulangi langkah 3 hingga 5 hingga semua vertex dikunjungi
Contoh:
a) Jika ada jalur yang menghubungkan, tolak (continue).
b) Jika belum ada jalur, terima, masukkan ke T.
Stop jika semua vertex sudah dilewati (Jumlah edges di T jumlahnya sudah jumlah vertex-1).
Shortest Path - Djikstra's Algorithm
Shortest Path adalah metode yang digunakan untuk menemukan jalur terpendek dari graph dengan vertex awal dan akhir yang spesifik. Bisa dicari dengan menggunakan Algoritma Djikstra.
Penjelasan:
1. Pilih simpul sumber (simpul awal)
2. Tentukan N sebagai set kosong
3. Beri label simpul awal dengan 0, dan masukkan ke dalam N
4. Ulangi langkah 5 hingga 7 hingga simpul tujuan berada di N atau tidak ada mode berlabel node di N.
5. Pertimbangkan setiap simpul yang tidak dalam N dan terhubung oleh tepi dari simpul yang baru dimasukkan.
6.
a) Jika node yang tidak dalam N tidak memiliki label maka SET label label = label dari node yang baru dimasukkan + panjang tepi
b) Jika node yang tidak dalam N sudah diberi label, maka SET label baru = minimum (label titik baru dimasukkan + panjang tepi, label lama)
7. Pilih satu simpul yang bukan di N yang memiliki label terkecil yang ditugaskan padanya dan tambahkan ke N.
Contoh:
Demikian materi data structure yang saya pelajari di semester 2 ini. Mohon maaf jika ada kekurangan atau kesalahan. Terima kasih terkhusus pada dosen Pak Henry dan Pak Ferdinand yang telah memberikan ilmu kepada saya dan mahasiswa fakultas Teknik Informatika.
Angelia
2301854492
Hari: Senin, 15/06/2020
Kelas: CB01
Lecturer:
- Henry Chong (D4460)
- Ferdinand Ariandy Luwinda (D4522)
- Ferdinand Ariandy Luwinda (D4522)
Referensi:
PPT Binus Maya
Zoom Meeting
Link web belajar lainnya
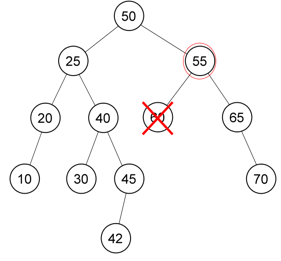
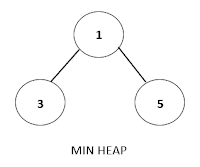
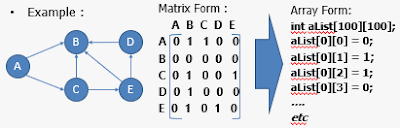
Comments
Post a Comment